Understanding Elementary Shapes Class 6 Maths NCERT Chapter 5

Key Features of NCERT Material for Class 6 Maths Chapter 5 – Understanding Elementary Shapes
In previous chapter 4, we studied the basic geometrical ideas of Lines, line segments, angles, and different shapes. In chapter 5 of class 6 NCERT maths book: Understanding Elementary Shapes, we will look at understanding more about elementary shapes like triangle, polygon, circles, etc. and the measurements of their line segments, angles, and vertices.
Quick revision notes
All the shapes we see around us are framed utilizing curves or lines. We can see corners, edges, planes, open and closed curves in our environment. We arrange them into line segments, angles, triangles, polygons, and circles. it could be seen that they don’t have a similar measure. So it is important to create devices to compare their sizes.
Measuring Line
A line segment is a fixed part of a line. In this way, we can quantify a line segment. The separation between the endpoints of a line segment called its length. The measurement of a line section is a unique number. In fact, the measure of a line segment is called its length. It assists us in comparing two line sections.
This should be possible in a few different ways as below:
- Comparing by observation
- Correlation by tracing
- Correlation utilizing a ruler and a divider.
There are four primary directions. Those are North (N), South (S), East (E) and West (W).
The turn from north to east forms a right angle. The turn from north to the south forms two right angles. It is known as a straight angle.
On the off chance that we turn by two straight angles or four right angles in a similar way, at that point it makes a full turn and we arrive at our original position. This one full turn is called one revolution. And the angle for one revolution is a complete angle.
We can see these revolutions on clock faces. At the point when the hand of a clock moves to start with one position then onto the next, it turns through an angle. Assume the hand of a clock begins at 12 and goes around until it arrives at 12 once more. So, it has made one revolution. It turned through one complete angle or two straight angles or four right angles.
Angles– Acute, Obtuse, and Reflex
The angle lesser than a right angle is known as the acute angle. An angle is known as an obtuse angle when it’s lesser than a straight angle but larger than a right angle.
An angle is known as a reflex angle when it is greater than the straight angle.
Acute angle:
An angle littler than a right angle is called an acute angle. An acute angle is less than a quarter of a revolution. (<90)
Obtuse angle:
An angle bigger than a right angle however lesser than a straight angle is called an obtuse angle. An is more than a quarter of revolution but less than half of the revolution. (>90;<180)
Reflex angle:
A reflex angle is bigger than a straight angle. (>180)
Measuring Angles
To look at two angles precisely, we need the measurements of them. This can be done with the assistance of a protractor. One complete revolution is segregated into 360 parts. Each part is known as a degree. The measure of the angle is known as ‘degree measure’. We compose 360 degrees as 360°.
Perpendicular Lines
When two lines intersect each other and the angle formed between them is a right angle, then they are known as perpendicular lines. In the event that a line AB is perpendicular to line CD, at that point we write AB ⊥ CD.
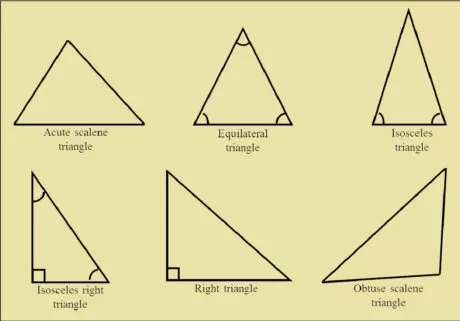
Classification of Triangles
We are aware that a triangle is a polygon with the least number of sides. There are various sorts of triangles.
Triangles can be characterized based on their edges as follows:
- When each angle in a triangle is acute, it is called an acute-angled triangle.
- In the event that any angle of a triangle is a right angle, it is known as a right-angled triangle.
- In the event that anyone angle in a triangle is obtuse, it is called an obtuse-angled triangle.
The triangles can likewise be grouped based on the lengths of their sides as follows:
- In the event that all three sides of a triangle are not of equal length, it is known as a scalene triangle.
- If any two of the sides of a triangle are equivalent, it is called an isosceles triangle.
- By chance that all three sides of a triangle are of equivalent length, it is called a symmetrical triangle.
Quadrilaterals
In this chapter: Understanding Elementary Shapes, we know that a quadrilateral is a four-sided polygon. A quadrilateral has four angles, four sides, and two diagonals. Quadrilaterals can be classified in accordance with their properties as follows:
In the event that the quadrilateral has just one set of parallel sides, at that point, the quadrilateral is known as a trapezium.
In the event that it has two pairs of parallel, at that point, the quadrilateral is known as a parallelogram.
Polygons
We realize that a polygon of 3 sides is known as a triangle and a polygon of 4 sides is known as a quadrilateral, More numbers of sides in a polygon could be found. We may arrange the polygons as indicated by the quantity of their sides. A polygon of 5 sides is known as a pentagon, a polygon of 6 sides is known as a hexagon and a polygon of 8 sides is called an octagon.
Circles
A simple closed curve which is not a polygon is called a circle. When a point moves from a fixed distance at a fixed point it forms a circle. The fixed middle point in a circle is called the centre. The perimeter of a circle or the distance moved by point along the circle is called its circumference.
Three Dimensional Shapes
We see around us numerous three-dimensional shapes. Cubes, cuboids, spheres, cylinders, cones and pyramids are a few of them.
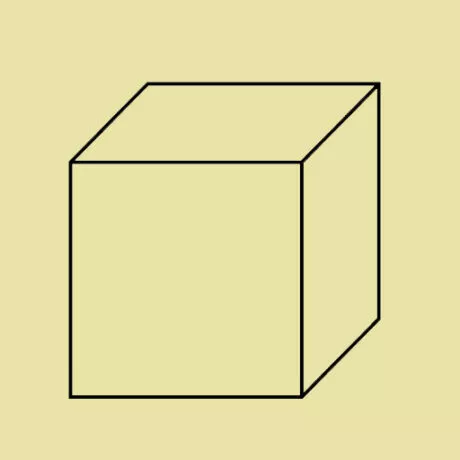
Cubes
Each side is known as a face, Two faces meet in a line segment called an edge. Three edges meet at a point known as the vertex.
Prism
It has one of its faces as a triangle. So it is known as a triangular prism. The triangular face is called it’s base. A prism has two same bases. Its other different faces are parallelograms. When a prism has a rectangular base, it is known as a rectangular prism, (or cuboid).
Pyramid
It is a shape with one base. The rest of the faces are triangles. When the base face is a triangle, it is known as a triangular pyramid. When the base face is a square, it is known as a square pyramid.


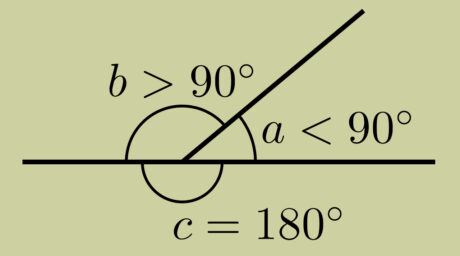
0 responses on "Understanding Elementary Shapes Class 6 Maths NCERT Chapter 5"