Carbon and its Compounds:Class 10 Science NCERT Chapter 4

Key Features of NCERT Material for Class 10 Science Chapter 4 – Carbon and its Compounds
In the previous Chapter 3:Metals and non metals we have seen the properties of bothmeta and non metal.In this Chapter 4:Carbon and its compounds,we will learn about the properties of carbon compound and the basics of organic chemistry
Quick revision notes
Bonding in Carbon
The Covalent bond, Electron spot structure, Physical properties of natural mixes, Allotropes of Carbon.
Covalent Bond: The nuclear number of carbon is 6. Its electronic arrangement is 2, 4. It requires 4 electrons to accomplish the inactive gas electronic arrangement. However, carbon can’t shape an ionic bond
It could increase four electrons shaping C4-cation. Yet, it would be hard for the core with six protons to clutch ten electrons.
It could lose four electrons shaping C4+ cations. Yet, it requires a lot of vitality to eliminate four electrons.
Along these lines, carbon conquers this issue by sharing of its valence electrons with other carbon iotas or with particles of different components.
The bond shaped by common sharing of electron sets between two particles in an atom is known as Covalent Bond.
Sorts of Covalent Bond:
Single Covalent Bond: When a solitary pair of electrons are shared between two particles in an atom. For instance; F2, Cl2, H2 and so on.
Twofold Covalent Bond: When two sets of electrons are shared between two iotas in a particle. For instance; O2, CO2 and so forth.
Triple Covalent Bond: When three sets of electrons are shared between two particles in an atom. For instance; N2 and so on.
Electron Dot Structure: The electron dab structures gives an image of holding in atoms as far as the mutual sets of electrons and octet rule.
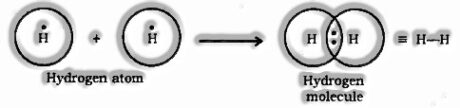
Development of Hydrogen Molecule
Nuclear number of Hydrogen = 1
Number of valence electrons = 1
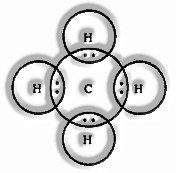
Formation of CH4 Molecule
Carbon atomic number = 6 [2, 4]
Valence electrons = 4
Hydrogen atomic number = 1
valence electrons = 1
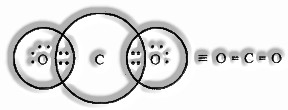
Formation of CO2 Molecule
Carbon atomic number = 6 [2, 4]
valence electrons = 4
Oxygen atomic number = 8 [2, 6]
valence electrons = 6
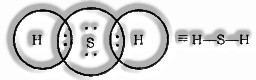
Formation of H2S Molecule
Sulphur atomic number= 16 [2, 8, 6]
valence electrons = 6
Physical Properties of Organic Compounds
The majority of the organic compounds have low bubbling and softening point, because of the feeble force of fascination (i.e., the between atomic force of fascination) between these particles.
Most carbon compounds are helpless conduits of power, because of the nonappearance of free electrons and free particles.
| Compounds | M.P. (K) | B.P. (K) |
| Acetic acid (CH3COOH) | 290 | 391 |
| Chloroform (CHCl3) | 209 | 334 |
| Ethanol (CH3CH2OH) | 156 | 351 |
| Methane (CH4) | 90 | 111 |
Allotropes of Carbon
Allotropy: The marvel where the component exists in at least two distinctive physical states with comparative compound properties are called Allotropy.
Carbon has Three Main Allotropes
- Diamond: In this, carbon, a molecule is clung to four different particles of carbon framing three-dimensional structures. It is the hardest substance and an encasing. It is utilized for boring rocks and cutting. It is likewise utilized for making gems.
- Graphite: In this, every carbon molecule is clung to three other carbon particles. It is a decent conduit of power and utilized as a grease.
- Buckminster Fullerene: It is an allotrope of the carbon-containing group of 60 carbon iotas combined to frame circular atoms. It is dim strong at room temperature.
Flexible nature of Carbon, Hydrocarbons, Isomerism, Homologous arrangement, Functional gatherings, Nomenclature of utilitarian gatherings.
Flexible Nature of Carbon: The presence of such an enormous number of natural mixes is because of the accompanying idea of carbon,
Catenation
Tetravalent nature.
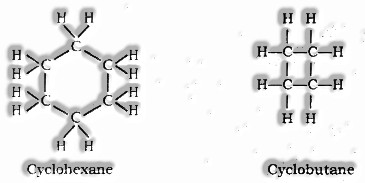
(i) Catenation: oneself connecting property of a component for the most part carbon molecule through covalent bonds to frame long straight, extended and rings of various sizes are called Catenation.
This property is expected to
- The little size of the carbon particle.
- The incredible quality of the carbon-carbon bond.
Carbon can likewise frame stable various bonds (twofold or triple) with itself and with the particles of different components.
Straight Chain
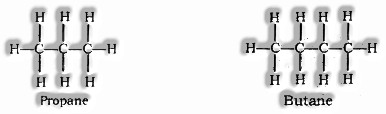
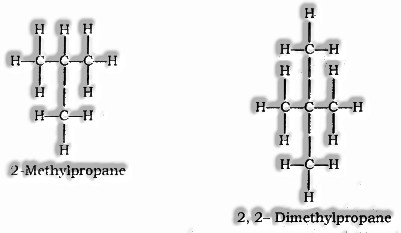
Branched Chain
Rings
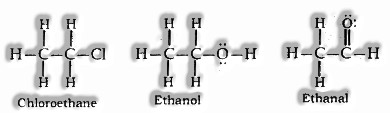
(ii) Tetravalent Nature: Carbon has valency of four. It is equipped for holding with four different particles of carbon or some different heteroatoms with single covalent bond just as twofold or triple bond.
Hydrocarbons: Hydrocarbons are compounds of hydrogen and carbon.
For example; Methane (CH4), Ethane (C2H6), Ethene (C2H4), Ethyne (C2H2) etc.
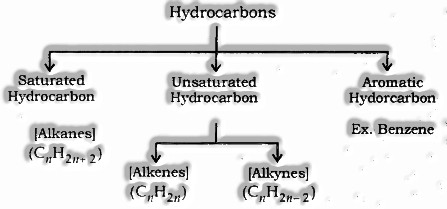
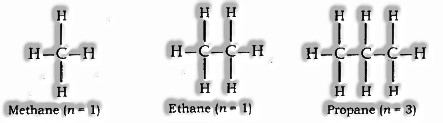
Saturated Hydrocarbon (Alkanes): CnH2n+2 is the General formula
Where, n = number of carbon atoms.
In this, a single bond connects carbon atom
For example; Methane (CH4), Ethane (C2H6) etc.
Unsaturated Hydrocarbons
Alkenes: CnH2n is General formula, where n = number of carbon atoms.
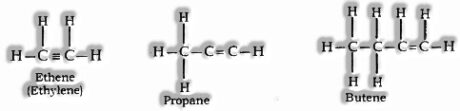
In this, the two carbon atoms are connected by double bond.
Alkynes: General formula is CnH2n-2, where n = number of carbon atoms. In this, the two carbon atoms are connected by triple bond.
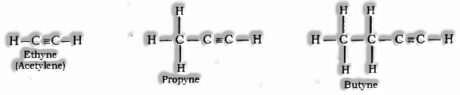
Electron Dot Structure of Hydrocarbons
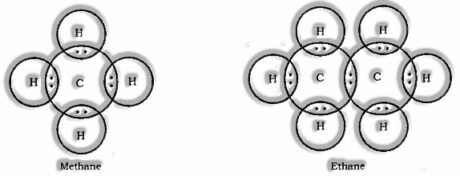
Isomerism: Compounds having similar atomic recipe however extraordinary auxiliary equation and properties are known as Isomers and this marvel is known as Isomerism.
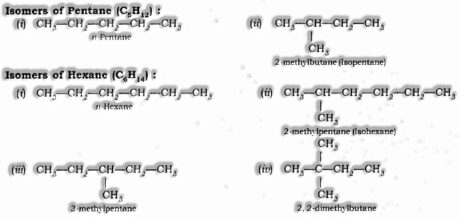
Structural Isomerism: Compounds having similar sub-atomic equation yet various structures are called Structural isomers. Model: Isomers of butane (C4H10)

Homologous Series: Arrangement of natural mixes having similar practical gathering and synthetic properties and progressive individuals contrast by a CH2 unit or 14 mass units are known as Homologous arrangement.
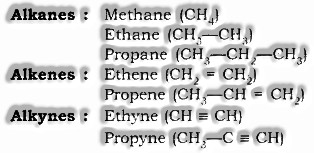
Homologous arrangement of Alkanes, Alkenes and Alkynes
Characteristics for Homologous Series
- The progressive individuals in homologous arrangement vary by CH2 unit or 14 mass unit.
- Individuals from given homologous arrangement have a similar functional group.
- All the individuals from homologous arrangement shows comparable substance properties.
Functional Group: A particle or group of iotas present in an atom which to a great extent decides its substance properties are called Functional Group.

![]()
Nomenclature of Organic Compounds: It is hard to recollect a great many mixes by their individual regular name. Along these lines, to organize the nomenclature of natural mixes IUPAC (International Union of Pure and Applied Chemistry) has given certain standard which is as per the following:
- Distinguish the Number of Carbon Atoms in the Compound
| S. No | Number of Carbon Atoms | Word Root (-) (Suffix) | Single bond |
| 1. | One carbon atoms (1-C) | Meth | + ane |
| 2. | Two carbon atoms (2-C) | Eth | + ane |
| 3. | Three carbon atoms (3-C) | Prop | + ane |
| 4. | Four carbon atoms (4-C) | But | + ane |
| 5. | Five carbon atoms (5-C) | Pent | + ane |
| 6. | Six carbon atoms (6-C) | Hex | + ane |
- Distinguish the functional group
| S. No. | Functional Group | Prefix | Suffix |
| 1. | Double bond (=) | — | ene |
| 2. | Triple bond (≡) | — | yne |
| 3. | Chlorine (—Cl) | Chloro | — |
| 4. | Bromine (—Br) | Bromo | — |
| 5. | Alcohol (-OH) | — | ol |
| 6. | Aldehyde (-CHO) | — | al |
| 7. | Ketone (-CO-) | — | one |
| 8. | Carboxylic acid (-COOH) | — | oic acid |
- Name the Compounds By Following Order
Prefix + Word Root + Suffix


Chemical Properties of Carbon Compounds
- Combustion: The total combustion of carbon compounds in the air gives carbon dioxide water, warmth and light.
CH3CH2OH(l) + O2(g) → CO2(g) + H2O(l) + Heat and light
Carbon consumes in air or oxygen to give carbon dioxide and warmth and light.
C(s) + O2(g) → CO2(g) + Heat and light
Immersed hydrocarbons ignite with a blue fire within the sight of an adequate flexibly of air or oxygen.
CH4(g) + 2O2(g) → CO2(g) + 2H2O(l) + Heat and light
In nearness of restricted flexibly of air, immersed hydrocarbon shapes a dingy fire.
Unsaturated hydrocarbons ignite with a yellow smoky fire.
The gas and lamp fuel oven utilized at home has bay for air so that, consumed to given clean blue fire.
Because of quality of limited quantity of nitrogen and sulfur, coal and oil produces carbon dioxide with oxides of nitrogen and sulfur which are significant poison.
- Oxidation: Oxidation of ethanol in nearness of oxidizing operators gives ethanoic acid.

Oxidizing Agent: A few substances are equipped for adding oxygen to other people, are known as Oxidizing Agent.
Example: Alkaline KMnO4 (or KMnO4—KOH)
Acidified K2Cr2O7 (or K2Cr2O7—H2SO4)
KMnO4 – Potassium permanganate
K2Cr2O7 – Potassium dichromate
- Addition Reaction: Expansion of dihydrogen with unsaturated hydrocarbon within the sight of impetuses, for example, nickel or platinum or palladium are known as Hydrogenation (expansion) response.
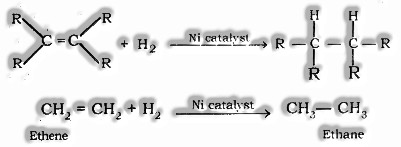
Catalyst: Substances that cause a response to happen or continues to various rate without devouring in it are known as an catalyst. For instance; Ni, Pt, Pd, and so on.
Cycle of changing over vegetable oil into strong fat (vegetable ghee) is called Hydrogenation of Oil.
Vegetable oil + H2 ![]() Vegetable ghee
Vegetable ghee
Vegetable fats are saturated fats which are harmful for health.
Vegetable oil containing unsaturated fatty acids are good for health.
- Substitution Reaction: Substitution of at least one hydrogen iota of a natural particle by another molecule or gathering of the molecule is known as Substitution Reaction.

Some Important Carbon Compounds :
Ethanol (CH3CH2—OH): Commonly known as Ethyl Alcohol.
Physical Properties
- It is drab, inflammable fluid.
- It is miscible with water in all extents.
- It has no impact on the litmus paper.
Chemical Properties
- Reaction with sodium
![]()
- Reaction with concentrated H2SO4 (Dehydration Reaction)
![]()


