Algebra Class 6 Maths NCERT Chapter 11

Key Features of NCERT Material for Class 6 Maths Chapter 11 – Algebra

In the previous chapter 10 mensuration, we studied about the perimeter and area of different figures.

In chapter 11 of NCERT class 6 maths: Algebra, We will look at what are variables and constants, application of variables in other branches of mathematics. We’ll also learn what are equations and how to solve them.

Quick revision notes

The branch of mathematics wherein we study numbers is called arithmetic. The branch of mathematics wherein we study shapes is called geometry. Similarly,  Algebra is also a branch of mathematics

In Algebra, there is the use of letters. We substitute letters for numbers to find the unknown. Utilization of letters helps in many ways as follows: 

• Utilizing letters we can write rules and formulae in a general manner. 
• Utilizing letters we can discuss any number and not only a specific number. 
• The letters may represent unknown amounts. By learning ways of determining unknowns, we grow integral assets for solving puzzles and many problems from day to day life. 
• Since letters represent numbers, we can perform operations on them as on numbers. This prompts the study of algebraic expressions and their properties.  

Matchstick Patterns 

We can make letters and different shapes utilizing matchsticks. We can write an equation between the quantity of matchsticks required for duplicating a given shape. The number of times a given shape is duplicated changes; it takes on values 1, 2, 3,…. It is a variable, signified by some letter n. 

The Idea of a Variable 

Variable is an unknown quantity that can vary(or change). The value of a variable isn’t constant. It can take various values. For instance, the length of a square can have any value. Hence, it is a variable. But the number of sides of a square has fixed value 4. So, it can’t be termed as a variable. We may utilize any letter n, l, m, p, x, y, z, and so forth to show a variable. 

Constant

A constant is a known quantity. It has a fixed value. It can be any numerical value.

More Matchstick Patterns 

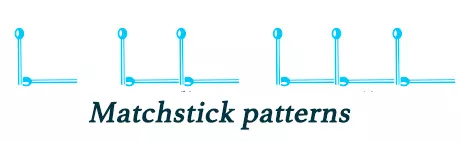We can make numerous letters of the alphabets and different shapes from matchsticks. For instance M, L, Triangle, Square, and so forth. In a matchstick pattern, we utilize the variable n to give us the overall rule for the number of matchsticks needed to make a pattern. This is a significant utilization of Variables in Mathematics. 

More Examples of Variables 

To show a variable, we may utilize any letter as n, m, l, p, x,y, z, and so forth. Review that a variable is a number, which doesn’t have a fixed value. It can take on different values. For instance, the number 10, or the number 100 or some other given number is not a variable. It is a constant because they have fixed values. In the same way, the number of sides of a quadrilateral (4) is fixed; it is likewise not a variable. 

Utilization of Variables in Common Rules 

Rules from geometry 

• The perimeter of a square (p) = 4s, where s is the length of the side of the square
• The perimeter of a rectangle (p) = 2l + 2b, wherein l is the length and b is the breadth of the rectangle

Rules from Arithmetic 

• Commutativity of Addition 

Let a and b be two different variables, which can take any numerical value. 

At that point, a + b = b + a 

• Commutativity of Multiplication 

Let a and b be two different variables. 

At that point, a × b = b × a 

• Distributivity of multiplication over addition

Let a, b and c be three different variables. 

So, a × (b + c) = a × b + a × c 

• Associativity of addition

Let a, b and c be three different variables. 

At that point, (a + b) + c = a + (b + c). 

Expressions with Variables 

We realize that variables can take various values; they do not have a fixed value. But, they are still numbers. So, as in numbers operations of addition, subtraction, multiplication, and division can also be performed on them. Using various operations, we can form expressions with variables like x – 1, x + 3, 2n, 5m, 3y + 5, 3l – 8, and so on. 

Note:  The Expressions of numbers can be quickly assessed. 

For instance: 3 × 4 + 6 = 12 + 6 = 18 

Yet, the expression containing a variable cannot be solved until the variable has some value. 

For instance, 

At the point where x = 1, 4x + 3 = 4 × 1 + 3 = 4 + 3 = 7. 

Utilizing Expressions Practically 

Numerous statements depicted in ordinary language can be changed to expressions with variables. 

Equation

An equation is a condition on a variable. It is communicated by saying that expression with a variable is equivalent to a fixed number. 

For instance, x – 3 = 4. 

An equation has two different sides, LHS and RHS and between them, is an indication of correspondence (=). 

The Equation expresses that the estimation of the left-hand side (LHS) is equivalent to the estimation of the right-hand side (RHS). 

If LHS isn’t equivalent to the RHS, we don’t get an equation. 

For instance, the statement 2n > 10 or 2n < 10 isn’t an equation.

Note: A statement like 10 – 1 = 9 is known as a numerical equation as neither of its sides contains a variable. As a rule, the word equation is utilized distinctly for equations including at least one variable. 

 The solution of an Equation 

The value of the variable in an equation where LHS of the equation is equivalent to RHS of the equation and is said to fulfil the equation and itself is known as a solution of the equation. For instance, n = 3 is a solution for the equation 2n = 6, where n = 3 isn’t a solution of the equation 2n = 12. 

Getting a Solution to the Equation 

Trial and error method is one of the ways to get a solution to an equation. In this technique, we allocate some value to the variable and check whether it fulfils the equation. We continue doling out along these lines by assigning different values to the variable until we find the one that satisfies the equation. 

But, this is certainly not an immediate and useful method of finding a solution. We need less time consuming and a more systematic method for getting a solution to the equation than a trial and error method. In simple equations, the variable is replaced by a placeholder and its value if found out by the usual methods. So, the value of the variable that is received after solving is the solution of the equation. 

Using an Equation 

Initially, we are given an equation in a variable whose value is not known to us. The solution of the equation is the unknown value. In this manner a variable in a condition is viewed as unknown and beginning from the unknown, we can see up the equation. Solving the equation is the technique for finding the unknown. It is, in this manner, an incredible technique for solving puzzles and problems.