Surface Areas And Volumes: Class 10 Mathematics NCERT Chapter 13

Key Features of NCERT Material for Class 10 Mathematics Chapter 13 – Surface Areas and Volumes 

In the last chapter 12, you learned about Areas Related to Circles. In this chapter, Surface Areas and Volumes, you will learn everything about it.

Cuboid and its Surface Area 

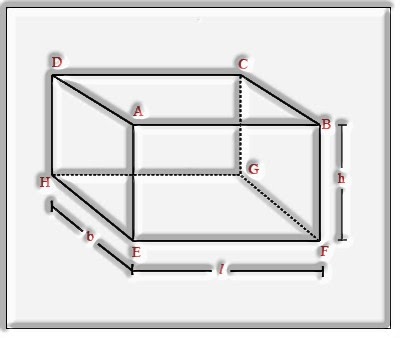
The surface area of a cuboid is equivalent to the total of the areas of its six rectangular faces. Consider a cuboid whose measurements are l × b × h individually. 

Cuboid that has length l, breadth b and height h 

The absolute surface area of the cuboid (TSA) = Sum of the areas of all its six faces 

TSA (cuboid) = 2(l × b) + 2(b × h) + 2(l × h) = 2(lb + bh + lh) 

Horizontal surface area (LSA) is the area of the apparent multitude of sides separated from the top and base faces. 

The parallel surface area of the cuboid = Area of face AEHD + Area of face BFGC + Area of face ABFE + Area of face DHGC 

LSA (cuboid) = 2(b × h) + 2(l × h) = 2h(l + b) 

Length of side of a cuboid =√(l2 + b2 + h2) 

Right Circular Cone and its Surface Area 

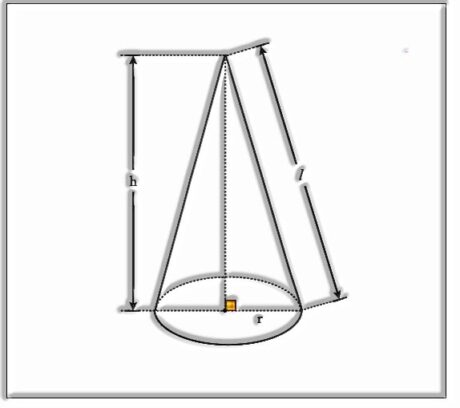
Think about a right angular cone with incline length l, radius r and height h. 

Cone with the base radius r and height h 

CSA of right round cone = πrl 

TSA is equal to CSA + area of base = πrl + πr2 = πr(l + r) 

Sphere and its Surface Area 

For a sphere of radius r 

Curved Surface Area (CSA) = complete Surface Area (TSA) = 4πr2 

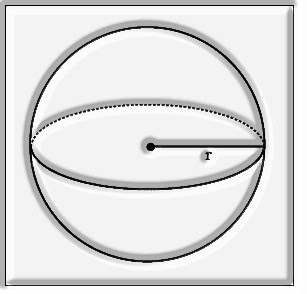
Sphere with radius r

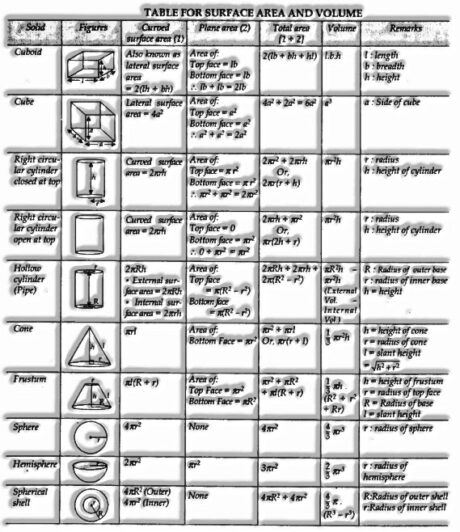
SURFACE AREA AND VOLUME OF COMBINATIONS 

Cone over a Cylinder. 

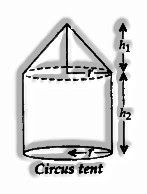
r = radius of cylinder and cone; 

h1 = height of the cone 

h2 = height of  cylinder 

All out Surface area is equal to Curved surface area of cone + Curved surface area of cylinder + area of round base 

= πrl + 2πrh2 +πr2; 

Inclination height,

Total Volume is equal to Volume of cone + Volume of cylinder 

Cone over a Hemisphere: 

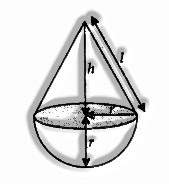
h = height of cone; 

l = incline height of cone =

r = radius of cone and hemisphere 

Total Surface area is equal to Curved surface area of cone + Curved surface area of hemisphere = πrl + 2πr2 

Volume is equal to Volume of cone + Volume of hemisphere = 

Funnel shaped Cavity in  Cylinder 

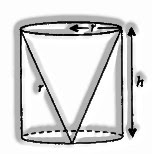
r = radius of cone and cylinder; 

h = height of cylinder and funnel shaped cavity; 

l = Slant height 

Total Surface area is equal to Curved surface area of cylinder + Area of base face of cylinder + Curved surface area of cone = 2πrh + πr2 + πrl 

Volume is equal to Volume of cylinder – Volume of cone 

Cones on Either Side of Cylinder. 

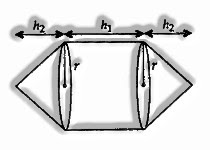
r = radius of cylinder and cone; 

h1 represents height of cylinder 

h2 represents height of cones 

Inclination height of cone, 

Surface area is equal to Curved surface area of 2 cones + Curved surface area of cylinder = 2πrl + 2πrh1 

Volume = 2(Volume of cone) + Volume of cylinder 

Cylinder with Hemispherical Ends. 

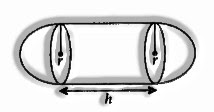
r = radius of cylinder and hemispherical closures; 

h = height of cylinder 

Total surface area is equal to Curved surface area of cylinder + Curved surface area of 2 hemispheres = 2πrh + 4πr2 

Volume is equal to Volume of cylinder + Volume of 2 hemispheres 

Hemisphere on Cube or Hemispherical Cavity on a Cube 

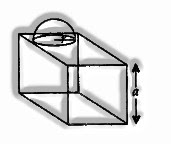
a = side of cube; 

r = radius of hemisphere. 

Surface area is equal to Surface area of a cube– Area of hemisphere face + Curved surface area of hemisphere 

= 6a2 – πr2 + 2πr2 = 6a2 + πr2 

Volume = Volume of a cube + Volume of hemisphere 

Hemispherical Cavity in Cylinder 

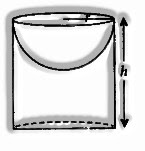
r = radius of hemisphere; 

h = height of cylinder 

Complete surface area = Curved surface area of cylinder + Surface area of base + Curved surface area of hemisphere 

= 2πrh + πr2 + 2πr2 = 2πrh + 3πr2 

Total Volume is equal to Volume of cylinder – Volume of hemisphere =