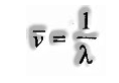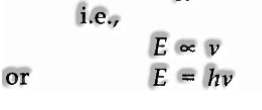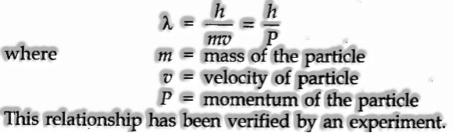Structure of Atom: Class 11 Chemistry NCERT Chapter 2
Key Features of NCERT Material for Class 11 Chemistry Chapter 2 – Structure of Atom
In the previous chapter of NCERT class 11 chemistry: Some Basic Concepts of Chemistry, you studied applications, laws and concepts of chemistry. In this chapter: Structure of Atom you will learn about parts of atoms and different theories associated with the discovery of the atom. Each atom has an atomic structure of which it is made up off. The atomic structure comprises of a positively charged nucleus and a negatively charged electron spinning around it.
Besides, to comprehend atomic structure we first need to comprehend what is an atom. Atom alludes to the exceptionally little molecule that isn’t noticeable to unaided eyes however is available all over. Additionally, an atom is the structural block of everything in this whole universe.
In addition, each strong, fluid and gas is comprised of the atom. Besides, without an atom, nothing can exist in the universe.
Components of the Atomic Structure
The atomic structure of an atom comprises of three particles that cooperate to make an atom. Following are the three segments of Atomic Structure –
Proton
Neutron
Electron
Quick revision notes
Discovery of Electron—Discharge Tube Experiment
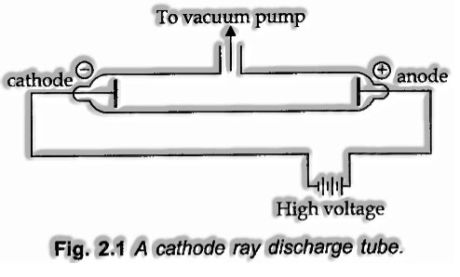
In 1879, William Crooks considered the conduction of power through gases at low weight. He played out the examination in a discharge tube which is a tube-shaped hard glass tube around 60 cm long. It is fixed at both the closures and fitted with two metal electrodes as appeared in Fig. 2.1.
The electrical discharge through the gases could be watched uniquely at low weights and at exceptionally high voltages.
The weight of various gases could be balanced by evacuation. At the point when adequately high voltage is applied over the electrodes, current beginnings coursing through a flood of particles moving in the tube from the negative electrode (cathode) to the positive electrode (anode). These were called cathode rays or cathode beam particles.
Properties of Cathode Rays
(I) Cathode rays move in a straight line.
(ii) Cathode rays start from the cathode and move towards the anode.
(iii) These rays themselves are not noticeable but rather their conduct can be seen with the assistance of particular sort of materials (fluorescent or luminous) which light when hit by them.
(iv) Cathode rays comprise of negatively charged particles. At the point when an electric field is applied on the cathode rays with the assistance of a couple of metal plates, these are seen as deflected towards the positive plate showing the nearness of negative charge.
(v) The qualities of cathode rays don’t rely on the material of electrodes and the nature of gas present in the cathode ray’tube.
Measurement of Charge/Mass (elm) Ratio for Electrons
J. Thomson tentatively decided charge/mass ratio called elm ratio for the electrons. For this, he oppressed the light emission delivered in the discharge tube as cathode rays to impact the electric and magnetic fields. These were acting opposite to each other just as to the way followed by electrons.
As indicated by Thomson, the measure of the deviation of the particles from their way in the nearness of electrical and magnetic field relies on the following variables:
(I) Greater the extent of the charge on the molecule, more prominent is the interaction with the electric or magnetic field and accordingly more noteworthy is the deflection.
(ii) The mass of the molecule — lighter the molecule, more prominent the deflection.
(iii) The deflection of electrons from their unique way increments with the expansion in the voltage over the electrodes or quality of the magnetic field.
Via completing precise estimations on the measure of deflections saw by the electrons on the electric field quality or magnetic field quality, Thomson had the option to decide the estimation of
e/me = 1.758820 x 1011 C kg-1 here me = Mass of the electron in kg
e = greatness of charge on the electron in coulomb (C).
Charge on the Electron
Robert Andrews Millikan conceived a technique known as an oil drop examination to decide the charge on the electrons.
Discovery of Proton—Anode Rays
In 1886, Goldstein altered the discharge tube by utilizing a punctured cathode. On diminishing the weight, he watched another sort of luminous rays going through the gaps or perforations of the cathode and moving in a direction inverse to the cathode rays. These rays were named as positive rays or anode rays or as channel rays. Anode rays are not radiated from the anode yet from space among anode and cathode.
Properties of Anode Rays
(I) The estimation of positive charge (e) on the particles establishing anode rays relies on the nature of the gas in the discharge tube.
(ii) The charge to mass ratio of the particles is found to rely upon the gas from which these start.
(iii) Some of the positively charged particles convey a different from the major unit of electrical charge.
(iv) The conduct of these particles in the magnetic or electric field is inverse to that watched for electron or cathode rays.
Proton
The littlest and lightest positive ion was acquired from hydrogen and was called a proton. Mass of proton is equal to 1.676 x 10-27 kg
Charge on a proton is equal to 1.602 x 10-19 C (+)
Neutron
It is neutral in nature molecule. It was found by Chadwick (1932).
By the barrage of flimsy sheets of beryllium with quick-moving a-particles, he watched
- that exceptionally infiltrating rays comprise of neutral particles which were named neutrons.
Thomson Model of Atom
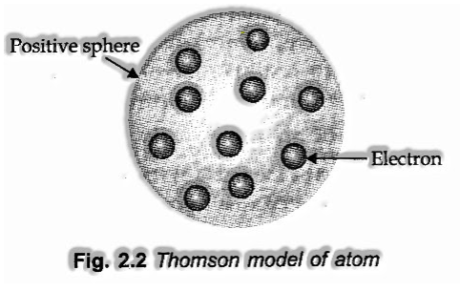
(I) J. J. Thomson recommended that an atom might be viewed as a sphere of assumed span 1CT8 cm conveying positive charge because of protons and in which negatively charged electrons are installed.
(ii) In this model, the atom is pictured as a pudding or cake of positive charge with electrons implanted into it.
(iii) The mass of an atom is viewed as uniformly spread over the atom as indicated by this model.
The drawback of Thomson Model of Atom
This model had the option to clarify the general lack of bias of the atom, it couldn’t agreeably, clarify the aftereffects of dissipating tests completed by Rutherford in 1911.
Rutherford’s a-molecule Scattering Experiment
Rutherford in 1911, played out some dispersing tests wherein he besieged dainty foils of metals like gold, silver, platinum or copper with a light emission moving a-particles. The slim gold foil had a ringed fluorescent zinc sulfide screen around it. At whatever point a-particles struck the screen, a minuscule blaze of light was created by then.
From these examinations, he mentioned the accompanying objective facts:
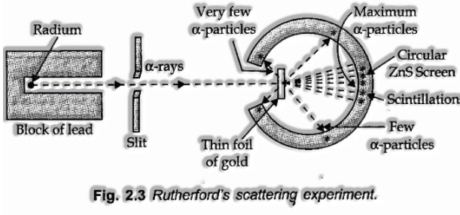
(I) Most of the a-particles went through the foil without experiencing any deflection,
(ii) two or three a-particles experienced deflection through little angles.
(iii) Very hardly any minor redirected back i.e., through an angle of almost 180°.
From these observations, Rutherford made the accompanying inferences:
(I) Since a large portion of the a-particles went through the foil without experiencing any deflection, there must be adequate void space inside the atom.
(ii) A little fraction of a-particles was avoided by little angles. The positive charge must be gathered in a little volume that repulsed and redirected a couple positively charged a-particles. This extremely little portion of the atom was called the nucleus.
(iii) The volume of the nucleus is extremely little when contrasted with the absolute volume of the atom.
Rutherford’s Nuclear Model of an Atom
(I) The positive charge and the vast majority of the mass of the atom were densely gathered in an amazingly little region. This little portion of the atom was called nucleus by Rutherford.
(ii) The nucleus is encircled by electrons that move around the nucleus with an exceptionally rapid in round ways called orbits.
(iii) Electrons and nucleus are stuck together by electrostatic powers of attraction.
Atomic Number
The number of protons present in the nucleus is equivalent to the atomic number (z). For instance, the number of protons in the hydrogen nucleus is 1, in sodium atom, it is 11, accordingly, their atomic numbers are 1 and 11. So as to grip the electrical neutrality, the number of electrons in an atom is equivalent to the number of protons (atomic number, z). For instance, the number of electrons in the hydrogen atom and sodium atom are 1 and 11 separately.
Atomic Number (z) = The number of protons in the nucleus( central) of an atom.
Is equal to Quantity of electrons in a neutral atom.
Mass Number
A number of protons and neutrons present in the nucleus are all things considered known as nucleons. The complete number of nucleons is named as mass number (An) of the atom.
Mass Number (A) = the number of protons in an atom (p) + Number of neutrons in an atom(n).
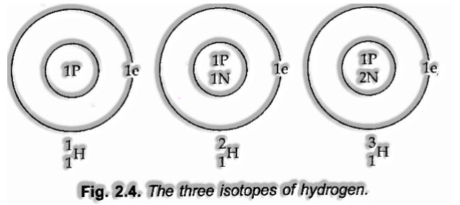
Isotopes
Atoms with an indistinguishable atomic number yet extraordinary atomic mass number are known as Isotopes.
Isotopes of Hydrogen:
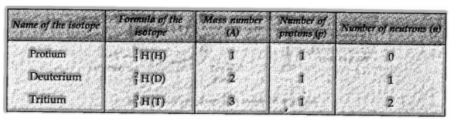
These three isotopes appear in the figure beneath:

Qualities of Isotopes
(I) Since the isotopes of a component have the equivalent atomic number, however unique mass number, the cores of isotopes contain a similar number of protons, yet an extraordinary number of neutrons.
(ii) Since the isotopes vary in their atomic masses, all the properties of the isotopes relying on the mass are extraordinary.
(iii) Since, the chemical properties are for the most part dictated by the number of protons in the nucleus, and the number of electrons in the atom, the various isotopes of a component display comparable chemical properties. For instance, all the isotopes of carbon on burning give carbon dioxide.
Isobars
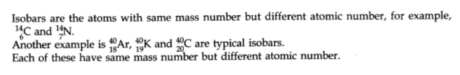
Drawbacks of Rutherford Model
(I) When a body is moving in a circle, it accomplishes acceleration. Hence, an electron moving around the nucleus in a circle is under acceleration.
As indicated by Maxwell’s electromagnetic hypothesis, charged particles when quickened must produce electromagnetic radiations. In this way, an electron in a circle will discharge radiations, the energy conveyed by radiation originates from electronic motion. Its way will turn out to be nearer to the nucleus and eventually should winding into the nucleus inside. 10-8 s. However, this doesn’t occur.
In this way, Rutherford’s model can’t clarify the stability of an atom if the motion of electrons is depicted based on traditional mechanics and electromagnetic hypothesis.
(ii) Rutherford’s model doesn’t give any thought regarding the distribution of electrons around the nucleus and about their energies.
Advancements Leading to the Bohr’s Model of Atom
Two developments assumed a significant job in the formulation of Bohr’s model of the atom. These were:
(I) The dual character of the electromagnetic radiation which implies that radiations have both wave-like and molecule like properties.
(ii) Experimental outcomes with respect to atomic spectra which can be clarified distinctly by accepting quantized electronic energy levels in atoms.
The character of Electromagnetic Radiation (Electromagnetic Wave Theory)
This theory was launched by James Clark Maxwell in 1864. The primary concerns of this theory are as per the following:
(I) The energy is transmitted from any source (like the warmed pole or the fibre of a bulb through which electric flow is passed) constantly as radiations and is the radiant energy.
(ii) The radiations include electric and magnetic fields oscillating perpendicular to one another and both perpendicular to the direction of propagation of the radiation.
(iii) The radiations hold wave character and travel with the velocity of light 3 x 108 m/sec.
(iv) These waves don’t require any material medium for propagation. For instance, rays from the sun contact us through space which is a non-material medium.
Characteristics of a Wave
Wavelength:
It is characterized as the distance between any two continuous peaks or troughs. It is symbolized by X and its S.I. unit is meter.
Frequency:
Frequency of a wave is characterized as the number of waves going through a point in one second. It is symbolized by v (nu) and is communicated in Hertz (Hz).
1 Hz = 1 cycle/sec.
Velocity:
The velocity of a wave is characterized as the direct distance went by the wave in one second.
It is symbolized by c and is communicated in cm/sec or m/sec.
Amplitude:
The amplitude of a wave is the stature of the peak or the profundity of the through. It is symbolized to by V and is communicated in the units of length.
Wave Number:
It is characterized as the number of waves present in 1-meter length. Clearly it will be equivalent to the corresponding of the wavelength. It is symbolized to by bar v (read as a nu bar).
Electromagnetic Spectrum:
When electromagnetic radiations are arranged by their expanding wavelengths or diminishing frequencies, the total spectrum acquired is called the electromagnetic spectrum.
Limitations of Electromagnetic Wave Theory
Electromagnetic wave theory was fruitful in clarifying properties of light, for example, obstruction, diffraction and so on; however it couldn’t clarify the accompanying:
(I) The phenomenon of dark body radiation.
(ii) The photoelectric impact.
(iii) The disparity of warmth capacity of solids as a function of temperature.
(iv) The line spectra of atoms regarding hydrogen.
Black Body Radiation
The perfect body, which emanates and retains all frequencies is known as a dark body and the radiation discharged by one such body is called dark body radiati
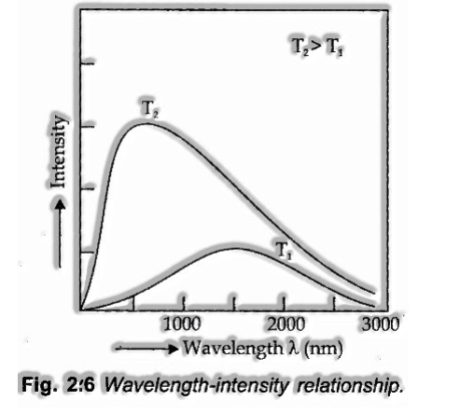
on. The. precise frequency distribution of the produced radiation from a dark body relies just upon its temperature.
At a given temperature, the intensity of radiation transmitted increments with the diminishing of wavelength arrives at the greatest value at a given wavelength and afterwards begins diminishing with a further reduction of wavelength as appeared in Fig 2.6.
Planck’s Quantum Theory
To clarify the phenomenon of ‘Dark body radiation’ and photoelectric impact, Max Planck in 1900, set forward a theory known as Planck’s Quantum Theory.
This theory was additionally stretched out by Einstein in 1905. The primary concerns of this theory were as per the following:
(I) The radiant energy produced or consumed as little bundles of energy. Each such parcels of energy are known as a quantum.
(ii) The energy of every quantum is legitimately proportional to the frequency of the radiation where his a proportionality constant, Planck’s constant. Its value is equivalent to 6.626 x 10-34 Jsec.
Photoelectric Effect
Hertz, in 1887, found that when light emission of certain frequency strikes the outside of certain metals, electrons are produced or launched out from the metal surface. The phenomenon is called photoelectric impact.
Observations in the Photoelectric Effect
(I) Only photons of light of certain base frequency called threshold frequency (v0) can cause the photoelectric impact. The value of v0 is distinctive for various metals.
(ii) The kinetic energy of the electrons which are transmitted is straightforwardly proportional to the frequency of the striking photons and is very autonomous of their intensity.
(iii) The number of electrons that are shot out every second from the metal surface relies on the intensity of the striking photons or radiations and not upon their frequency.
Explanation of the Photoelectric Effect
Einstein in (1905) gave an explanation of the various purposes of the photoelectric impact utilizing Planck’s quantum theory as under:
(I) Photoelectrons are catapulted just when the incident light has a specific least frequency (threshold frequency v0)
(ii) If the frequency of the occurrence light (v) is more than the threshold frequency (v0), the abundance energy (HV – hv0) is granted to the electron as kinetic energy.
K.E. of the launched out electron
The energy of the discharged electron.
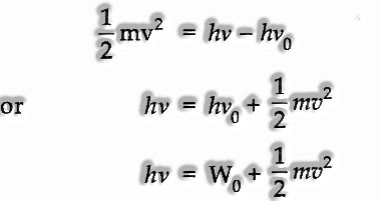
(iii) On expanding the intensity of light, more electrons are launched out yet the energies of the electrons are not adjusted.
Dual Behavior of Electromagnetic Radiation
From the analysis of the conduct of light, researchers reached the conclusion that light and other electromagnetic radiations have a double nature. These are wave nature just as molecule nature. At whatever point radiation interfaces with the matter, it shows molecule like properties as opposed to the wavelike properties (impedance and diffraction) which it displays when it proliferates. Some minuscule particles, similar to electrons, likewise show this wave-molecule duality.
Spectrum
At the point when a beam of white light is gone through a prism the wave with shorter wavelength twists more than the one with a more drawn out wavelength. Since conventional white light comprises of waves with all the wavelengths in the noticeable range, an exhibit of white light is spread out into a progression of shaded groups called a spectrum. The light of red shading which has the longest wavelength is veered off the least while the violet light, which has the briefest wavelength digresses the most.
Continuous Spectrum
At the point when a beam of white light is dissected by going through a crystal, it is seen that it separates into seven distinctive wide groups of hues from violet to red (like a rainbow). These hues are ceaseless to such an extent that every one of them converges into the following. Thus, the spectrum is called a continuous spectrum.
Emission Spectra
Emission Spectra is seen when the radiations transmitted from a source are gone through a prism and afterwards got on the photographic plate. Radiations can be discharged in a number of ways, for example,
(I) from the sun or sparkling electric bulb.
(ii) by letting electric discharge through a gas at low weight.
(iii) by warming a substance to high temperature.
Line Spectra
At the point when the fumes of some unpredictable substance are permitted to fall on the fire of a Bunsen burner and afterwards broke down with the assistance of a spectroscope. Some particular shaded lines show up on the photographic plate which is distinctive for various substances. For instance, sodium or its salts discharge yellow light while potassium or its salts give out a violet light.
Absorption Spectra
At the point when white light is gone through the fumes of a substance and the communicated light is then permitted to strike a crystal, dull lines show up in the generally continuous spectrum. The dark lines demonstrate that the radiations comparing to them were consumed by the substance from the white light. This spectrum is the absorption spectrum.
Dark lines show up precisely at similar positions where the lines in the emission spectra show up.
Line Spectrum of Hydrogen
At the point when an electric discharge is gone through hydrogen gas encased in discharge tube under low pressure and the produced light is examined by a spectroscope, the spectrum comprises of a huge number of lines which are assembled into the 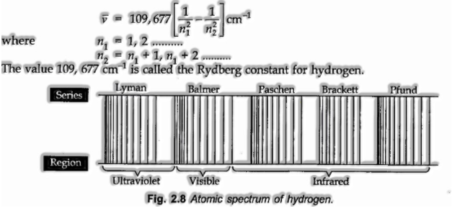
various arrangement. The total spectrum is known as the hydrogen spectrum.
Based on trial observations, Johannes Rydberg noticed that all arrangement of lines in the hydrogen spectrum could be depicted by the accompanying expression:
Rydberg in 1890, and has given a basic hypothetical equation for the calculation of wavelengths and wavenumbers of the spectral lines in the various arrangement of the hydrogen spectrum. The equation is known as the Rydberg recipe (or equation).
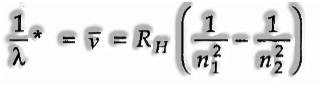
This relation is substantial for hydrogen atom as it were. For different species,
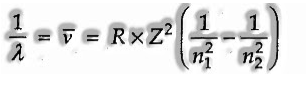
where Z is the symbol of the atomic number of the species.
Here RH = steady, called Rydberg consistent for hydrogen and n1, n2 are whole numbers (n2 > n1)
For a specific arrangement, the value of n1 is consistent while that of n2 changes.Take an instance,
For Lyman arrangement, n1= 1, n2= 2, 3, 4, 5… … ..
For Balmer arrangement, n1 = 2, n2 = 3, 4, 5, 6… … ..
For Paschen arrangement, n1= 3, n2 = 4, 5, 6, 7… … ..
The Brackett series,n1 = 4, n2 = 5, 6, 7, 8… … ..
For Pjund arrangement, n1 =5, n2 = 6, 7, 8, 9… … ..
Hence, by subbing the values of n1 and n2 in the above equation, wavelengths and wavenumber of various spectral lines can be determined. When n1 = 2, the expression gave above is called Balmer’s recipe.
Bohr’s Model of Atom
Niels Bohr in 1913, proposed another model of atom based on Planck’s Quantum Theory. The primary concerns of this model are as per the following:
(i) In an atom, the electrons rotate around the nucleus in certain unmistakable round ways called orbits.
(ii) Each circle is related to clear energy and in this manner, these are known as energy levels or energy shells. These are numbered as 1, 2, 3, 4… … .. or then again K, L, M, N… ….
(iii) Only those energy orbits are allowed for the electron where the precise force of the electron is an entire number various of h/2π
Angular momentum of the electron (mvr) is equal to nh/2π (n is equal to 1, 2, 3, 4 etc)
m = mass of the electron.
v = tangential velocity of the spinning electron.
r is the radius of the circle.
h stands for Planck’s constant.
n is a number.
(iv) As long as an electron is available in a specific circle, it neither retains nor loses energy and its energy, hence, stays consistent.
(v) When energy is provided to an electron, it retains energy just in fixed sums as quanta and bounces to higher energy state away from the nucleus known as energized state. The energized state is precarious, the electron may bounce back to the lower energy state and in doing as such, it radiates a similar measure of energy. (∆E = E2 – E1).
Achievements of Bohr’s Theory
- Bohr’s theory has clarified the soundness of an atom.
- Bohr’s theory has helped in computing the energy of an electron in the hydrogen atom and one electron animal groups. The numerical expression for the energy in the nth circle is,
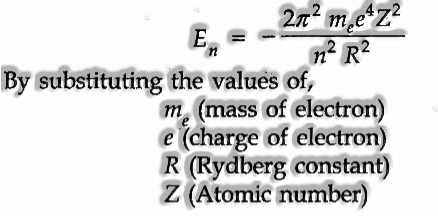
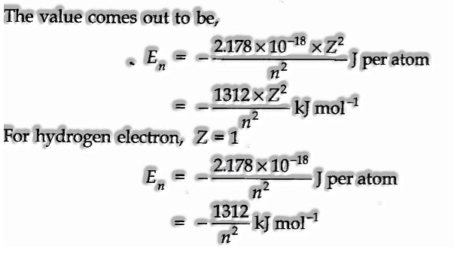
- Bohr’s theory has clarified the atomic spectrum of the hydrogen atom.
Limitations of Bohr’s Model
(I) The theory couldn’t clarify the atomic spectra of the atoms containing more than one electron or multielectron atoms.
(ii) Bohr7s theory neglected to clarify the fine structure of the spectral lines.
(iii) Bohr’s theory couldn’t offer any agreeable explanation of the Zeeman effect and the Stark effect.
(iv) Bohr’s theory neglected to clarify the capacity of atoms to shape particle framed by chemical bonds.
(v) It was not as per the Heisenberg’s uncertainty principle.
Twofold Behavior of Matter (de Broglie Equation)
de Broglie in 1924, recommended that issue, similar to radiation, ought to likewise display double conduct i.e., both molecule like and wave-like properties. This implies like photons, electrons have momentum and wavelength as well.
From this similarity, de Broglie gave the accompanying relation between wavelength (λ) and energy (p) of a material molecule.
Heisenberg’s Uncertainty Principle
It expresses that, “It is hard to decide at the same time, the specific position and definite energy (or velocity) of an electron”.
Significance of the Uncertainty Principle
(I) It precludes the presence of positive ways or directions of electrons and other comparative particles.
(ii) The impact of Heisenberg’s vulnerability guideline is critical just for infinitesimal articles and is unimportant for plainly visible items.
Causes for the Failure of the Bohr Model
(I) The wave character of the electron isn’t considered in the Bohr Model.
(ii) According to the Bohr Model, an orbit is an unmistakably characterized way and this way can totally be described just if both the position and the velocity of the electron are known precisely simultaneously. This is absurd as indicated by the Heisenberg’s uncertainty rule.
Quantum Mechanical Model of Atom
Quantum mechanics: Quantum mechanics is a hypothetical science that manages the investigation of the motions of the minuscule items that have both discernible wave-like and molecule like properties.
Significant Features of Quantum Mechanical Model of Atom
(I) The energy of electrons in an atom is quantized i.e., can just have certain values.
(ii) The presence of quantized electronic energy level is an immediate consequence of the wave-like properties of electrons.
(iii) Both the specific position and definite velocity of an electron in an atom can’t be resolved at the same time.
(iv) An atomic orbital has wave function φ. There are numerous orbitals in an atom. Electron possesses an atomic orbital which has distinct energy. An orbital can’t have multiple electrons. The orbitals are dispatched in expanding request of energy. All the information about the electron in an atom is put away in orbital wave function φ.
(v) The probability of discovering electron at a point inside an atom is proportional to the square of orbital wave function i.e., |φ2|at that point. It is known as probability density and is consistently positive.
From the value of φ2 at various focuses inside the atom, it is conceivable to anticipate the region around the nucleus where electron most likely will be found.
Quantum Numbers
Atomic orbitals can be determined by giving their comparing energies and precise forces which are quantized (i.e., they have explicit values). The quantized values can be communicated as far as a quantum number. These are utilized to get total information about electron i.e., its location, energy, turn and so on.
Head Quantum Number (n)
It is the most significant quantum number since it tells the central energy level or shell to which the electron has a place. It is indicated by the letter V and can have any fundamental value with the exception of zero, i.e., n = 1, 2, 3, 4… … .. and so forth.
The different head energy shells are additionally assigned by the letters, K, L, M, N, O, P … .. and so forth. Beginning from the nucleus.
The foremost quantum number gives us the accompanying information:
(I) It gives the normal distance of the electron from the nucleus.
(ii) It totally decides the energy of the electron in the hydrogen atom and hydrogen-like particles.
(iii) The most extreme number of electrons present in any chief shell is given by 2n2 where n is the number of the chief shell.
Azimuthal or Subsidiary or Orbital Angular Quantum Number (l)
It is discovered that the spectra of the components contain the fundamental lines as well as there are many almost negligible differences additionally present. This number assists with clarifying the scarce differences of the spectrum.
The azimuthal quantum number gives the accompanying information:
(I) The number of subshells present in the fundamental shell.
(ii) The precise energy of the electron present in any subshell.
(in) The overall energies of different subshells.
(iv) The states of the different subshells present inside a similar chief shell.
This quantum number is meant by the letter T. For a given value of n, it can have any value extending from 0 to n – 1. Take an instance,
For the first shell (k), n = 1, l can have just 1 value i.e., l = 0 For n = 2, the conceivable value of l can be 0 and 1.
Subshells relating to various values of l are expressed to by the accompanying images:
amount of l 0 1 2 3 4 5 … ..
System for subshell s p d f g h ……
Magnetic Orbital Quantum Number (m or m1)
The magnetic orbital quantum number decides the number of favoured orientations of the electrons present in a subshell. Since every orientation relates to an orbital, along these lines, the magnetic orbital quantum number decides the number of orbitals present in any subshell.
The magnetic quantum number is meant by letter m or ml and for a given value of l, it can have all the values extending from – l to + l including zero.
Hence, for the energy value of l, m has 2l + 1 values.
For instance,
For l = 0 (s-subshell), ml can have just one value i.e., m1 = 0.
This implies s-subshell has just a single orientation in space. As such, s-subshell has just a single orbital called s-orbital.
Spin Quantum Number (S or ms)
This quantum number assists in clarifying the magnetic properties of the substances. A turning electron carries on like a micro magnet with a clear magnetic second. On the off chance that an orbital contains two electrons, the two magnetic minutes contradict and drop one another.
Shapes of s-orbitals
s-orbital is available in the s-subshell. For this particular subshell, l = 0 and ml = 0. In this manner, s-orbital with just a single orientation has a circular shape with uniform electron thickness along with all the three tomahawks.
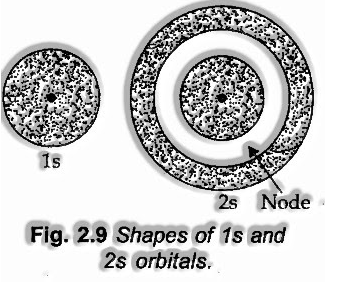
The likelihood of Is electron is seen as most extreme close to the nucleus and diminishes with the expansion out yonder from the nucleus. In the 2s electron, the likelihood is likewise greatest close to the nucleus and diminishes to zero likelihood. The circular void shell for 2s electron is called nodal surface or basically hub.
Shapes of p-orbitals
p-orbitals are available in the p-subshell for which l = 1 and m1 can have three potential orientations – 1, 0, + 1.
In this manner, there are three orbitals in the p-subshell which are assigned as px, py and Pz orbitals relying on the hub along which they are coordinated. The overall state of a p-orbital is hand weight comprising of two portions known as flaps. In addition, there is a plane going through the nucleus along which finding the electron thickness is nearly nil. This is referred to as nodal plane as appeared in the fig.
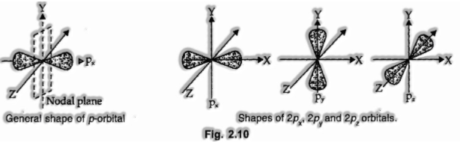
From the free weight pictures, it is very evident that not at all like s-orbital, a p-orbital is directional in nature and henceforth it impacts the states of the particles in the formation of which it takes an interest.
Shapes of d-orbitals
d-orbitals are available in d-subshell for which l = 2 and m[ = – 2, – 1, 0, +1 and +2. This implies there are five orientations prompting five distinctive orbitals.
Aufbau Principle
The guideline states: In the ground condition of the atoms, the orbitals are dispatched arranged by their expanding energies.
As it were, electrons initially possess the most reduced energy orbital accessible to them and go into higher energy orbitals simply after the lower energy orbitals are filled.
The request wherein the energies of the orbitals increment and henceforth the request where the orbitals are filled is as per the following:
This is 2s, 2p, 3s, 3p, 4s, 3d, 4p, 5s, id, 5p, 6s, if, 3d, 6p, 7s, 5f 6d, 7p
The request might be recalled by utilizing the strategy given in fig. 2.11.

Pauli Exclusion Principle
As per this guideline, no two electrons in an atom can have a similar arrangement of four quantum numbers.
Pauli exclusion guideline can likewise be expressed as: Only two electrons may exist in the equivalent orbital and these electrons must have inverse spins.
Hund’s Rule of Maximum Multiplicity
It expresses that: blending of electrons in the orbitals having a place with the equivalent subshell (p, d or f) doesn’t occur until each orbital having a place with that subshell has got one electron each i.e., it is separately involved.
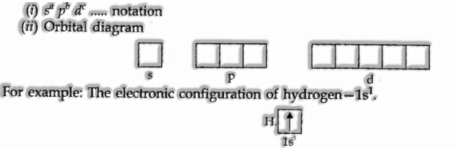
Electronic Configuration of Atoms
The scattering of electrons into orbitals of an atom is called its electronic configuration. The electronic configuration of various atoms c
For instance:
Roots of Stability of Completely Filled and Half Filled Subshells
The totally filled and half-filled subshells are steady because of the accompanying reasons:
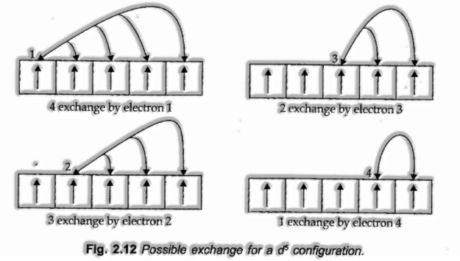

- Even distribution of electrons: The totally filled or half-filled subshells have balanced distribution of electrons in them and are consequently more steady.
- The balancing out impact emerges at whatever point at least two electrons with the same spin are available in the degenerate orbitals of a subshell. These electrons will in general trade their positions what’s more, the energy delivered because of their exchange is called exchange energy. The number of trades that can happen is most extreme when the subshell is either half-filled or totally filled. therefore the exchange energy is most extreme as is security.
Questions
- Which among the accompanying can move openly without connecting itself to an atom?
- Electron
- Proton
- Neutron
- The entirety of the abovementioned
Answer. The right answer is option A. It is one of the fundamental properties of an electron that can exist in nature in a free state. Additionally, it can connect itself with a component at the period of scarcity.