Some Applications of Trigonometry: Class 10 Mathematics NCERT Chapter 9

Key Features of NCERT Material for Class 10 Mathematics Chapter 9 – Some Applications of Trigonometry 

In the last chapter 8, you learned about Introduction of Trigonometry. In this chapter, you will learn about Applications of Trigonometry.

In mathematics, trigonometry is one of the most significant branches. Hence, the utilization of trigonometry incorporates, estimating the heights of pinnacles, deciding the distance of the item in the sea from the shore, finding the distance between celestial bodies, and so on. Basically, we use trigonometry to gauge heights and distances. Accordingly, we utilize trigonometric ratios to gauge heights and distances of various items. 

Line of Sight 

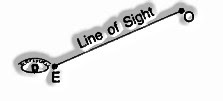
At the point when an eyewitness looks from a point E (eye) at an article O then the straight line EO between the eye E and the item O is known as the line of sight. 

Horizontal

At the point when a spectator looks from a point E (eye) to another point Q which is flat to E, at that point the straight line, EQ among E and Q is known as the horizontal line. 

Angle of Elevation 

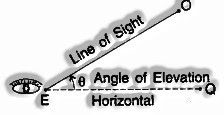
At the point when the eye is beneath the item, at that point the eyewitness needs to turn upward from the point E to the article O. The ratio of this pivot (angle θ) from the flat line is known as the angle of elevation. 

Angle of Depression 

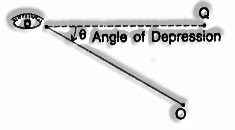
At the point when the eye is over the item, at that point the spectator needs to peer down from the point E to the article. The level line is presently parallel to the ground. The proportion of this turn (angle θ) from the even line is known as the angle of depression. 

Instructions to change over the above diagram with the right-angled triangle. 

The case I: Angle of Elevation is known 

Attract OX perpendicular to EQ. 

Presently ∠OXE = 90° 

ΔOXE is a right triangle. where 

OE = hypotenuse 

OX= opposite side (Perpendicular) 

EX = adjacent side (Base) 

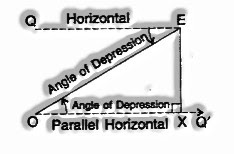
Case II: Angle of Depression is known 

(I) Draw OQ’parallel to EQ 

(ii) Draw perpendicular EX on OQ’. 

(iii) Now ∠QEO = ∠EOX = Interior alternate angles 

ΔEXO is a right Δ. where 

EO = hypotenuse 

OX= adjacent side (base) 

EX = opposite side (Perpendicular) 

Pick a trigonometric ratio so that it considers the known side and the side that you wish to compute. 

The eye is constantly considered at ground level except if the issue explicitly gives the stature of the spectator. 

The article is constantly considered as a point. 

A few People have 

Sin θ =

Wavy Black Hair 

Cos θ =

Turning Permanent Black. 

Tan θ =

Points to remember : 

• The angle of elevation is numerically equivalent to the angle of depression. They are consistently acute angles. 
• Both the angles are estimated with the even level. 
• To decide the not known side of the right triangle where one side is known and the acute angle is known. So we consolidate both the sides with trigonometric ratios of the triangle. For example

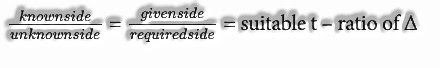
Figuring Heights and Distances 

To, figure heights and distances, we can utilize trigonometric ratios. 

Stage 1: Draw a line graph comparing to the issue. 

Stage 2: Mark every known tallness, distances and angles to find lengths by factors. 

Stage 3: Use the estimations of different trigonometric ratios of the angles to acquire the obscure lengths from the known lengths. 

Estimating the distances of Celestial bodies with the assistance of trigonometry 

Enormous distances can be estimated by the parallax technique. The parallax angle is a large portion of the angle between two lines of sights when an item is seen from two distinct positions. Realizing the parallax angle and the distance between the two positions, huge distances can be estimated.