Relations and Functions:Class 11 Maths NCERT Chapter 2

Key Features of NCERT Material for Class 11 Maths Chapter 2 – Relations and Functions

In the previous Chapter 1: Sets we have learned about sets,its types and some operations.In this chapter 2:Relations and functions we will study about the relations between the two objects in the pair.

Quick revision notes

Ordered Pair 

An ordered pair comprises of two articles or components in a provided fixed request. 

Equity of Two Ordered Pairs 

Two ordered pairs (a, b) and (c, d) are equivalent if a = c and b = d. 

Cartesian Product of Two Sets 

For any two non-void sets An and B, the arrangement of every single ordered pair (a, b) where a ∈ An and b ∈ B is known as the cartesian product of sets An and B and is meant by A × B. Accordingly, A × B = {(a, b) : a ∈ An and b ∈ B}. If A = Φ or B = Φ, at that point we characterize A × B = Φ 

Note: 

• A × B ≠ B × A 
• If n(A) = m and n(B) = n, at that point n(A × B) = mn and n(B × A) = mn
• If atleast one of A and B is infinite, then (A × B) is infinite and (B × A) is boundless.

Relations 

A relation R from a non-void set A to a non-void set B is a subset of the cartesian product set A × B. The subset is inferred by portraying a relationship between the primary component and the second component of the ordered pairs in A × B. 

The set of all first components in a relation R is known as the domain of the relation B, and the set of all subsequent components called pictures is known as the range of R. 

Note: 

• A relation might be spoken to either by the Roster form or by the set of builder form, or by an arrow diagram which is a visual portrayal of relation. 
• If n(A) = m, n(B) = n, at that point n(A × B) = mn and the absolute number of potential relations from set A to set B = 2mn 

Inverse of Relation 

For any two non-void sets An and B. Leave R alone a relation from a set A to a set B. At that point, the Inverse of relation R, indicated by R-1 is a relation from B to An and it is characterized by R-1 ={(b, a) : (a, b) ∈ R} 

Domain of R = Range of R-1 and 

Range of R = Domain of R-1.

Functions 

A relation f from a set A to set B is supposed to be function, if each component of set A has one and only picture in set B. 

As it were, a function f is a relation with the end goal that no two pairs in the relation have the principal component. 

Real-Valued Function 

A function f : A → B is known as a real-valued function if B is a subset of R (set of every single real number). If An and B both are subsets of R, at that point f is known as a real function. 

Some Specific Types of Functions 

Identity function: The function f : R → R characterized by f(x) = x for every x ∈ R is called identity function. 

Domain of f = R and Range of f = R 

Constant function: The function f : R → R characterized by f(x) = C, x ∈ R, where C is a constant ∈ R, is known as a constant function. 

Domain of f = R and Range of f = C 

Polynomial function: A real valued function f : R → R characterized by f(x) = a0 + a1x + a2x2+… + anxn, where n ∈ N and a0, a1, a2,… … .. a ∈ R for every x ∈ R, is called a polynomial function. 

Rational function: These are the real function of type , where f(x)and g(x)are polynomial functions of x characterized in a domain, where g(x) ≠ 0.

The modulus function: The real function f : R → R defined by f(x) = |x|

or

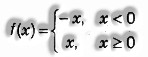
for all estimations of x ∈ R is known as the modulus function. 

Domain of f = R and Range of f = R+ U {0} for example [0, ∞) 

Signum function: The real function f : R → R characterized 

by f(x) = , x ≠ 0 and 0, if x = 0

or then again

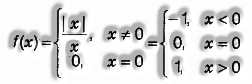
is called the signum function.

Domain of f = R and Range of f = {-1, 0, 1}

Greatest integer function: The real function f : R → R characterized by f (x) = {x}, x ∈ R expect that the estimations of the best number not exactly or equivalent to x, is known as the greatest integer function.. 

Domain of f = R and Range of f = Integer 

Fractional part function: The real function f : R → R characterized by f(x) = {x}, x ∈ R is known as the fractional part function.

f(x) = {x} = x – [x] for all x ∈R

Domain of f = R and Range of f = [0, 1)

Algebra of Real Functions

Addition of two real valued functions: Let f : X → R and g : X → R be any two real functions, where X ∈ R. At that point, we portray (f + g) : X → R by 

{f + g) (x) = f(x) + g(x), for all x ∈ X. 

Subtraction of a real valued function from another: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. At that point, we characterize (f – g) : X → R by (f – g) (x) = f (x) – g(x), for all x ∈ X. 

Multiplication by a scalar: Let f : X → R be a real function and K be any scalar having a place with R. At that point, the product of Kf is function from X to R characterized by (Kf)(x) = Kf(x) for all x ∈ X. 

Multiplication of two real valued functions: Let f : X → R and g : X → R be any two real functions, where X ⊆ R. At that point, product of these two functions for example f.g : X → R is characterized by (fg) x = f(x) . g(x) ∀ x ∈ X. 

Quotient of two real functions: Let f and g be two real functions characterized from X → R. The quotient of f by g signified by is a function characterized from X → R as