Quadratic Equations: Class 10 Mathematics NCERT Chapter 4

Key Features of NCERT Material for Class 10 Mathematics Chapter 4 – Quadratic Equations 

In the last chapter 3, you learned about Pair of Linear Equations in Two Variables. In this chapter: Quadratic Equations you will learn in detail about Quadratic Equations.

Quadratic Equation 

At the point when we compare a quadratic polynomial to a constant, we get a quadratic equation. 

Any equation of the structure p(x)=c, where p(x) is a polynomial of degree 2 and c is a constant, is a quadratic equation. 

A quadratic polynomial of the structure ax² + bx + c, where a ≠ 0 and a, b, c are real numbers, is known as a quadratic equation 

when ax² + bx + c = 0. 

Here an and b are the coefficients of x² and x individually and ‘c’ is said to be a  constant term. 

Any value is a solution of a quadratic equation if and just on the off chance that it fulfills the quadratic equation. 

Quadratic formula

: The roots, that are α and β of a quadratic equation ax² + bx + c = 0 are given 

by or given b² – 4ac ≥ 0. 

Here, the worth b² – 4ac is known as the discriminant and is by and large represented by D. ‘D’ encourages us to determine the idea of roots for a given quadratic equation. Subsequently D = b² – 4ac. 

The standards are: 

In the event that D = 0 ⇒ The roots are Real and Equivalent. 

In the event that D > 0 ⇒ The two roots are Real and not equal. 

In the event that D < 0 ⇒ No Real roots are there. 

In the event that α and β are the roots of the quadratic equation, at that point Quadratic equation is x² – (α + β) x + αβ = 0 Or x² – (whole of roots) x + product of roots = 0 

where,  addition of roots (α + β) =

Multiplication of roots (α x β) =

Solving QE by Factorisation 

Roots of a Quadratic equation 

The estimations of x for which a quadratic equation is fulfilled are known as the roots of the quadratic equation. 

In the event that α is a base of the quadratic equation ax2+bx+c=0, at that point aα2+bα+c=0. 

A quadratic equation can have two particular real roots, two equivalent roots or real roots may not exist. 

Graphically, the roots of a quadratic equation are the points on the graph where the chart of the quadratic polynomial cuts the x-axis. 

Consider the below graph of a quadratic equation x2−4=0: 

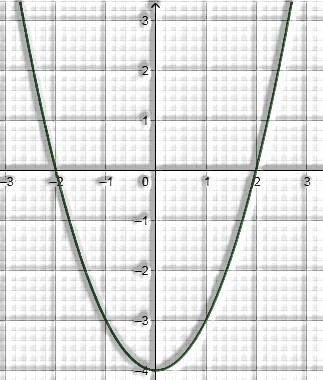
Chart of a Quadratic Equation 

In the figure given above, – 2 and 2 are the roots of the quadratic equation x2−4=0 

Note: 

• In the event that the diagram of the quadratic polynomial cuts the x-axis at two unmistakable focuses, at that point it has real and particular roots. 
• On the off chance that the diagram of the quadratic polynomial contacts the x-axis, at that point it has real and equivalent roots. 
• On the off chance that the diagram of the quadratic polynomial doesn’t cut or contact the x-axis then it doesn’t have any real roots. 

Solving a Quadratic Equation by Factorization technique 

Consider a quadratic equation 2×2−5x+3=0 

⇒2×2−2x−3x+3=0 

This progression is parting the center term 

We split the center term by discovering two numbers (- 2 and – 3) with the end goal that their entirety is equivalent to the coefficient of x and their item is equivalent to the product of the coefficient of x2 and the constant. 

(- 2) + (- 3) = (- 5) 

Furthermore, (- 2) × (- 3) = 6 

2×2−2x−3x+3=0 

2x(x−1)−3(x−1)=0 

(x−1)(2x−3)=0 

In this progression, we have communicated the quadratic polynomial as a result of its elements. 

In this manner, x = 1 and x =3/2 are the roots of the given quadratic equation. 

This strategy for tackling a quadratic equation is known as the factorisation technique.