Probability: Class 12 Mathematics NCERT Chapter 13

Key Features of NCERT Material for Class 12 Maths Chapter 13 – Probability

In the previous chapter 12, you learned about Linear Programming. In this chapter, you all will learn about probability.

Quick revision notes

Event: A subset of the sample space related with a random experiment is called an event or a case.

 for example In tossing a coin, getting either head or tail is an event.

Equally Likely Events: The given events are supposed to be equally likely if none of them is relied upon to happen in inclination to the next. 

for example In tossing a fair die, all the six faces are equally liable to come. 

Mutually Exclusive Events: A lot of events is supposed to be mutually exclusive, if the incident of one avoids the occurrence of the other, for example on the off chance that An and B are mutually exclusive, at that point (A ∩ B) = Φ 

for example In tossing a die, all the 6 faces numbered 1 to 6 are mutually exclusive, since in the event that any of these faces comes, at that point the chance of others in a similar trial is precluded. 

Exhaustive Events: A lot of events is supposed to be exhaustive if the exhibition of the experiment consistently brings about the event of at any rate one of them. 

On the off chance that E1, E2, … , En are exhaustive events, at that point E1 ∪ E2 ∪… … ∪ En = S. 

for example In tossing of two dice, the exhaustive number of cases is 62 = 36. Since any of the numbers 1 to 6 on the primary die can be related with any of the 6 numbers on the other die. 

Complement of an Event: Let A be an event in a sample space S, at that point the complement of An is the arrangement of all sample purposes of the space other than the sample point in An and it is signified by A’or . 

for example A’ = {n : n ∈ S, n ∉ A] 

Note: 

(I) An activity which brings about some all around characterized results is called an experiment. 

(ii) An experiment where the results may not be the equivalent regardless of whether the experiment is acted in an indistinguishable condition is known as a random experiment.

Probability of an Event 

On the off chance that a trial result is n exhaustive, mutually exclusive and equally likely cases and m of them are positive for the occurrence of an event An, at that point the probability of occurring of An is given by

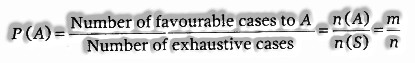
Note:

(i) 0 ≤ P(A) ≤ 1

(ii) Probability of an impossible event is zero.

(iii) Probability of certain events (possible event) is 1.

(iv) P(A ∪ A’) = P(S)

(v) P(A ∩ A’) = P(Φ)

(vi) P(A’)’ = P(A)

(vii) P(A ∪ B) = P(A) + P(B) – P(A ∩ S)

Conditional Probability: Let E and F be two events related with a similar sample space of a random experiment. At that point, probability of event of event E, when the event F has happened, is known as a Conditional probability of event E over F and is indicated by P(E/F)

.

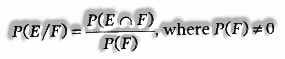
Similarly, the conditional probability of event F over E is given as

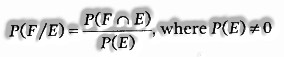
Properties of Conditional Probability: If E and E are two events of sample space S and G is an event of S which has just happened with the end goal that P(G) ≠ 0, at that point 

(I) P[(E ∪ F)/G] = P(F/G) + P(F/G) – P[(F ∩ F)/G], P(G) ≠ 0 

(ii) P[(E ∪ F)/G] = P(F/G) + P(F/G), if E and F are disjoint events. 

(iii) P(F’/G) = 1 – P(F/G) 

(iv) P(S/E) = P(E/E) = 1 

Multiplication Theorem: If E and F are two events related with a sample space S, at that point the probability of concurrent event of the events E and F is 

P(E ∩ F) = P(E) . P(F/E), where P(F) ≠ 0 

or on the other hand 

P(E ∩ F) = P(F) . P(F/F), where P(F) ≠ 0 

This outcome is known as multiplication rule of probability. 

Multiplication Theorem for More than Two Events: If F, F and G are three events of sample space, at that point 

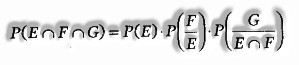
Independent Events: Two events E and F are supposed to be independent, if probability of event or non-event of one of the events isn’t influenced by that of the other. For any two independent events E and F, we have the connection 

(I) P(E ∩ F) = P(F) . P(F) 

(ii) P(F/F) = P(F), P(F) ≠ 0

(iii) P(F/F) = P(F), P(F) ≠ 0

Additionally, their complements are independent events, 

for example P( ∩ ) = P() . P() 

Note: If E and F are reliant events, at that point P(E ∩ F) ≠ P(F) . P(F).

Three events E, F and G are supposed to be mutually independent, if 

(I) P(E ∩ F) = P(E) . P(F) 

(ii) P(F ∩ G) = P(F) . P(G) 

(iii) P(E ∩ G) = P(E) . P(G) 

(iv)P(E ∩ F ∩ G) = P(E) . P(F) . P(G) 

In the event that atleast one of the above isn’t valid for three given events, at that point we state that the events are not independent. 

Note: Independent and mutually exclusive events don’t have a similar significance.

Baye’s Theorem and Probability Distributions 

Partition of Sample Space: A set of events E1, E2,… ,En is said to represent a partition of the sample space S, on the off chance that it satisfies the accompanying conditions: 

(I) Ei ∩ Ej = Φ; I ≠ j; where I, j = 1, 2, … .. n 

(ii) E1 ∪ E2 ∪ … ∪ En = S

(iii) P(Ei) > 0, where  I = 1, 2,… , n 

Theorem of Total Probability: Let events E1, E2, … , En structure a partition of the sample space S of an experiment.If An is any event associated with sample space S, at that point 

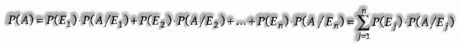
Baye’s Theorem: If E1, E2,… ,En are n non-void events which constitute a partition of sample space S, for example E1, E2,… , En are pairwise disjoint E1 ∪ E2 ∪ … . ∪ En = S and P(Ei) > 0, where I = 1, 2, … .. n Also, let A be any non-zero event, the probability 

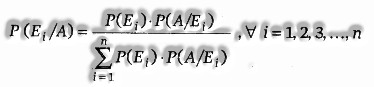
Random Variable: A random variable is a real-valued function, whose domain is a sample space of a random experiment. By and large, it is signified by capital letter X. 

Note: More than one random variables can be characterized in the same sample space. 

Probability Distributions: The system where the values of a random variable are given alongside their corresponding probabilities is called probability distribution. 

Leave X alone a random variable which can take n values x1, x2,… , xn. 

Let p1, p2,… , pn be respective probabilities. 

At that point, a probability distribution table is given as follows: 

where p1 + p2 + p3 +… + pn = 1 

Note: If xi is one of the possible values of a random variable X, at that point statement X = xi is genuine just at some point(s) of the sample space. Subsequently ,the probability that X takes esteem x, is always non-zero, for example P(X = xi) ≠ 0 

Mean and Variance of a Probability Distribution: Mean of a probability distribution is 

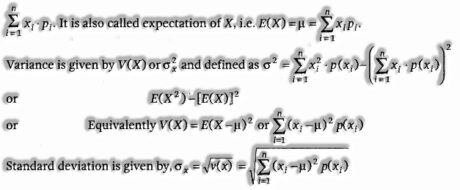
Bernoulli Trial: Trials of a random experiment are called Bernoulli trials on the off chance that they satisfy the accompanying conditions: 

(I) There should be a limited number of trials. 

(ii) The trials should be independent. 

(iii) Each trial has precisely two outcomes, success or failure. 

(iv) The probability of success remains the same in every trial. 

Binomial Distribution: The probability distribution of numbers of successes in an experiment consisting of n Bernoulli trials got by the binomial expansion (p + q)n, is called binomial distribution. 

Leave X alone a random variable which can take n values x1, x2,… , xn. At that point, by binomial distribution, we have P(X = r) = nCr prqn-r 

where, 

n = Total number of trials in an experiment 

p = Probability of success in one trial 

q = Probability of failure in one trial 

r = Number of success trial in theexperiment 

Also, p + q = 1 

Binomial distribution of the quantity of successes X can be represented as 

Mean and Variance of Binomial Distribution

(i) Mean(μ) = Σ xipi = np

(ii) Variance(σ2) = Σ xi2 pi – μ2 = npq

(iii) Standard deviation (σ) = √Variance = √npq

Note: Mean > Variance