Matrices:Class 12 Maths NCERT Chapter 3

Key Features of NCERT Material for Class 12 Maths Chapter 3 – Matrices

In the previous Chapter 2:Inverse trigonometric functions we will see basic concepts of inverse trigonometric functions.In this Chapter 3:Matrices we will study about matrix and its different properties.

Quick revision notes

Matrix:A matrix is an arranged rectangular exhibit of numbers or functions. The numbers or functions are known as the components or the sections of the matrix. 

Request of a Matrix: If a matrix has m lines and n segments, at that point its request is composed as m × n. In the event that a matrix has request m × n, at that point it has mn components. 

All in all, am×n matrix has the accompanying rectangular array: 

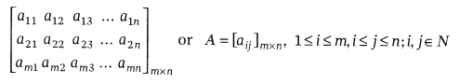
Note: We shall consider only those matrices, whose elements are real numbers or functions taking real values.

Types of Matrices

Column Matrix: A matrix that has only one column, is called a column matrix.

e.g.

In general, A = [aij]m×1 is a column matrix of order m × 1.

Row Matrix: A matrix that has only one row, is called a row matrix,

e.g.

In general, A = [aij]1×n is a row matrix of order 1 x n

Square Matrix: A matrix that has equivalent number of rows and columns, is called a square matrix

e.g.

In general, A = [aij]m x m is a square matrix of order m.

Note: If A = [aij] is a square matrix of order n, at that point elements a11, a22, a33,…, ann is said to comprise the diagonal of the matrix A.

Diagonal Matrix:A square matrix whose all the components aside from the diagonal components are zeroes, is known as a diagonal matrix, 

e.g.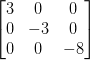

In general, A = [aij]m×m is a diagonal matrix, if aij = 0, when i ≠ j.

Scalar Matrix:A diagonal matrix whose all diagonal components are same (non-zero), is known as a scalar matrix, 

for example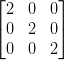

By and large, A = [aij]n×n is a scalar matrix, if aij = 0, when I ≠ j, aij = k (consistent), when I = j. 

Note: A scalar matrix is a diagonal matrix however a diagonal matrix might be a scalar matrix. 

Unit or Identity Matrix: A diagonal matrix where all diagonal components are ‘1’ and all non-diagonal components are zero, is called an identity matrix. It is signified by I. 

e.g.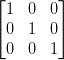

In general, A = [aij]n×n is an identity matrix, if aij = 1, when i = j and aij = 0, when i ≠ j.

Zero or Null Matrix: A matrix is supposed to be a zero or null matrix, if its all elements are zer0

e.g.

Equality of Matrices: Two matrices A and B are supposed to be equivalent, if

(i) order of A and B are same.

(ii) corresponding elements of A and B are same i.e. aij = bij, ∀ i and j.

e.g. and are equal matrices, but and are not equal matrices.

Operations on Matrices

Between at least two than two grids, the accompanying operations are characterized underneath:

Addition and Subtraction of Matrices:Addition and subtraction of two matrices are characterized in a request for both the networks are same. 

Addition of Matrix 

In the event that A = [aij]m×n and B = [yij]m×n, at that point A + B = [aij +bij]m×n, 1 ≤ I ≤ m, 1 ≤ j ≤ n 

Subtraction of Matrix 

In the event that A = [aij]m×n and B = [bij]m×n, at that point A – B = [aij – bij]m×n, 1 ≤ I ≤ m, 1 ≤ j ≤ n 

Properties of Addition of Matrices 

(a) Commutative If A = [aij] and B = [bij] are grids of a similar request say m x n then A + B = B + A, 

(b) Associative for any three frameworks A = [aij], B = [bij], C = [cij] of a similar request say m x n, A + (B + C) = (A + B) + C. 

(c) Existence of additive identity Let A = [aij] be amxn matrix and O be amxn zero matrix, at that point A + O = O + A = A. As it were, O is the additive identity for matrix addition. 

(d) Existence of additive inverse Let A = [aij]m×n be any matrix, at that point we have another matrix as – A = [-aij]m×n with the end goal that A + (- A) = (- A + A) = O. Along these lines, matrix (- An) is called additive inverse of An or negative of A. 

Note 

(I) If An and B are not of a similar request, at that point A + B isn’t characterized. 

(ii) Addition of networks is a case of a binary operation on the set of frameworks of a similar request. 

Multiplication of a matrix by scalar number: Let A = [aij]m×n be a matrix and k is scalar, at that point kA is another matrix gotten by increasing every component of A by the scalar k, for example on the off chance that A = [aij]m×n, at that point kA = [kaij]m×n. 

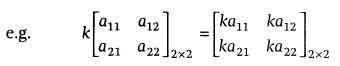
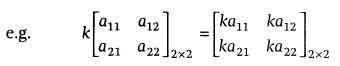
Properties of Scalar Multiplication of a Matrix 

Let A = [aij] and B = [bij]be two grids of a similar request say m × n, at that point 

(a) k(A + B) = kA + kB, when k is a scalar. 

(b) (k + l)A = kA + lA, where k and l are scalars. 

Multiplication of Matrices: Let An and B be two frameworks. At that point, their item AB is characterized, if the quantity of segments in matrix An is equivalent to the quantity of lines in matrix B. 

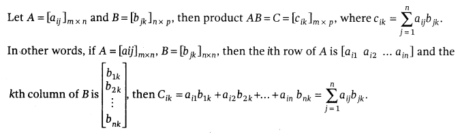
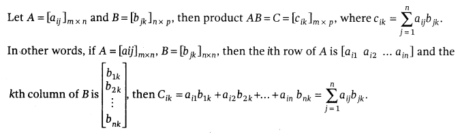
Properties of Multiplication of Matrices 

(a) Non-commutativity Matrix multiplication isn’t commutative for example on the off chance that AB and BA are both characterized, at that point it isn’t vital that AB ≠ BA. 

(b) Associative law For three grids A, B, and C, in the event that multiplication is characterized, at that point A (BC) = (AB) C. 

(c) Multiplicative identity For each square matrix A, there exists an identity matrix of a similar request with the end goal that IA = AI = A. 

Note: For Amxm, there is just a single multiplicative identity Im. 

(d) Distributive law For three frameworks A, B, and C, 

A(B + C) = AB + AC 

(A + B)C = AC + BC 

at whatever point the two sides of the equality are characterized. 

Note: If An and B are two non-zero frameworks, at that point their item might be a zero matrix. 

e.g. Assume A = and B = , then we have AB =