Vector Algebra: Class 12 Mathematics NCERT Chapter 10

Key Features of NCERT Material for Class 12 Maths Chapter 10 – Vector Algebra

In the last chapter 9, you learned about differential equations. In this chapter, you will learn everything about Vector Algebra.

Quick revision notes

Vector: Those quantities which have magnitude, just as direction, are called vector quantities or vectors. 

Note: Those quantities which have just magnitude and no direction, are called scalar quantities. 

Portrayal of Vector: A coordinated line segment has magnitude just as direction, so it is called vector meant as or essentially as . Here, the point A from where the vector begins is called its initial point and the point B where it ends is called its terminal point.

Magnitude of a Vector: The length of the vector or is called magnitude of or and it is written as || or || or a.

Note: Since, the length is never negative, then the notation ||< 0 has no significance.

Position Vector: Let O(0, 0, 0) be the root and P be a point in space having organizes (x, y, z) regarding the inception O. At that point, the vector or is known as the position vector of the point P as for O. The magnitude of or is given by

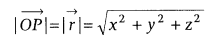
Direction Cosines: If α, β and γ are the angles which a coordinated line segment OP makes with the positive directions of the facilitate tomahawks OX, OY and OZ individually, at that point cos α, cos β and cos γ are known as the direction cosines of OP and are by and large meant by the letters l, m and n separately. 

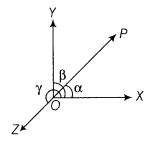
for example l = cos α, m = cos β, n = cos γ Let l, m and n be the direction cosines of a line and a, b and c be three numbers, with the end goal that Note: l2 + m2 + n2 = 1

Kind of Vectors

Null vector or zero vector: A vector, whose initial and terminal points harmonize and magnitude is zero, is known as a null vector and signified as .  Note: Zero vector can’t be doled out an unmistakable direction or it might be viewed as having any direction. The vectors , speak to the zero vector.

Unit vector: A vector of unit length is known as unit vector. The unit vector in the direction of is

Collinear vectors: At least two vectors are supposed to be collinear, in the event that they are parallel to a similar line, independent of their magnitudes and directions, for example and are collinear, when or

Coinitial vectors: At least two vectors having the same initial point are called coinitial vectors.

Equal vectors: Two vectors are supposed to be equivalent, on the off chance that they have equivalent magnitudes and same direction paying little heed to the position of their initial points. Note: If = , then but converse may not be true.

Negative vector: Vector having the same magnitude but inverse in direction of the given vector, is called the negative vector e.g. Vector is negative of the vector and represented as = – .

Note: The vectors characterized above are with the end goal that any of them might be dependent upon its parallel relocation without altering its magnitude and course. Such vectors are called ‘free vectors’. 

To Find a Vector when its Position Vectors of End Points are Given: Let a and b be the position vectors of end points A and B respectively of a given line segment AB. Then, = Position vector of – Positron vector of

= – = –

Addition of Vectors

Triangle law of vector addition: If two vectors are spoken to along different sides of a triangle taken all together, at that point their resultant is spoken to by the third side taken in inverse direction, for example in ∆ABC, by triangle law of vector addition, we have + = Note: The vector sum of three sides of a triangle taken in order is .

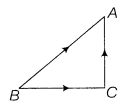
Parallelogram law of vector addition: If two vectors are spoken to along the two contiguous sides of a parallelogram, at that point their resultant is spoken to by the slanting of the sides. On the off chance that the sides OA and OC of parallelogram OABC speak to and separately, at that point we get

+ =

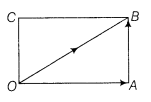
Note: Both laws of vector addition are identical to one another.

Properties of vector addition

Commutative: For vectors and , we have

Associative: For vectors , and , we have

Note: The associative property of vector addition empowers us to compose the sum of three vectors , and as without utilising brackets.

Additive identity: For any given vector , a zero vector is its additive identity as

Additive inverse: For a vector , a negative vector of is its additive inverse as

Multiplication of a Vector by a Scalar: Let be a given vector and λ be a scalar, at that point multiplication of vector by scalar λ, indicated as λ , is likewise a vector, collinear to the vector whose magnitude is |λ| times that of vector and direction is same as , if λ > 0, opposite of , if λ < 0 and zero vector, if λ = 0.

Note: For any scalar λ, λ . = .

Properties of Scalar Multiplication: For vectors , and scalars p, q, we have

(i) p( + ) = p + p

(ii) (p + q) = p + q

(iii) p(q ) = (pq)

Note: To demonstrate is parallel to , we need to show that = λ , where λ is a scalar.

Components of a Vector: Let the position vector of P concerning O is . This form of any vector is-called its component form. Here, x, y and z are called the scalar components of and , and are called the vector components of along the individual axes.

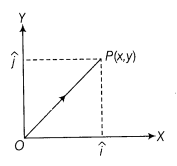
Two dimensions: If a point P in a plane has coordinates (x, y), at that point , where and are unit vectors along OX and OY-axes, separately.

At that point,

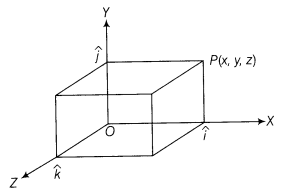
Three dimensions: If a point P in a plane has coordinates (x, y, z), at that point , where , and are unit vectors along OX, OY and OZ-axes, separately. At that point,

Vector Joining of Two Points: If P1(x1, y1, z1) and P2(x2, y2, z2) are any two points, at that point the vector joining P1 and P2 is the vector

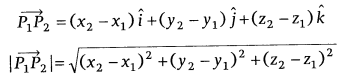
Section Formula: Position vector of point R, which partitions the line segment joining the points A and B with position vectors and separately, internally in the ratio m : n is given by

For external division,

Note: Position vector of mid-point of the line segment joining end points A() and B() is given by

Dot Product of Two Vectors: If θ is the edge between two vectors and , at that point the scalar or dot product denoted by .  is given by , where 0 ≤ θ ≤ π.

Note:

(i) is a real number

(ii) If either or , then θ is not characterized.

Properties of dot product of two vectors and are as per the following:

Vector (or Cross) Product of Vectors: If θ is the angle between two non-zero, non-parallel vectors and , then the cross product of vectors, denoted by is given by

where, is a unit vector perpendicular to both and , with the end goal that , and form a right handed system.

Note

(i) is a vector quantity, whose magnitude is

(ii) If either or , then0is not defined.

Properties of cross product of two vectors and are as follows: