Statistics: Class 11 Mathematics NCERT Chapter 15

Key Features of NCERT Material for Class 11 Maths Chapter 15 – Statistics

In the previous chapter 14, you learned about Mathematical Resoning. In this chapter, you will learn about Statistics and its uses.

Quick revision notes

Measure of Dispersion

The scattering is the measure of varieties in the estimations of the variable. It measures the level of scatteredness of the perception in a dissemination around the mean value.

Range

The proportion of scattering which is most effortless to comprehend and simplest to figure is the range.

 

Range is characterized as the distinction between two extraordinary observation of the circulation.

 

Range of dispersion = Largest observation – Smallest observation.

 

Mean Deviation

Mean deviation for ungrouped information

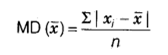
For n observations x1, x2, x3,… , xn, the mean deviation is given by

Mean scattering about their median M is given by

 

Mean deviation for discrete frequency distribution

Let the given information comprise of discrete observations x1, x2, x3,… … ., xn happening with frequencies f1, f2, f3,… … ., fn separately on the off chance that

Mean deviation about their Median M is given by

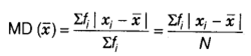
Mean deviation for continuous frequency distribution

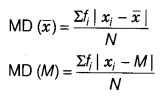
where xi are the mid-points of the classes,  and M are respectively, the mean and median of the distribution.

Variance

Variance is the number-crunching mean of the square of the deviation about mean .

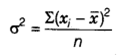
Let x1, x2, … xn be n observations with as the mean, at that point the variance signified by σ2, is given by

Standard deviation

The standard deviation is given by

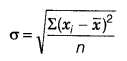
Standard deviation of a continuous frequency distribution is given by

Coefficient of Variation

So as to think about at least two recurrence disseminations, we look at their coefficient of variations. The coefficient of variation is characterized as

Note: The distribution having a more prominent coefficient of variation has greater fluctuation around the focal worth, at that point the distribution having a littler estimation of the coefficient of variation.