Real Numbers: Class 10 Mathematics NCERT Chapter 1

Key Features of NCERT Material for Class 10 Mathematics Chapter 1 – Real Numbers
In this years Mathematics we will learn some exciting concepts and theories. In the first chapter: Real Numbers, we will learn about Real numbers and their properties and get to know that how they can become useful to us.
R = Real Numbers:
All rational and irrational numbers are said to be real numbers.
I = Integers:
All numbers from (… – 3, – 2, – 1, 0, 1, 2, 3… ) are known as integers.
Q = Rational Numbers:
Real numbers of the structure, q ≠ 0, p, q ∈ I are rational numbers.
All integers can be communicated as rational, for instance, 6 = 6/1
Decimal expansion of rational numbers ending or non-ending recurring.
Q’ = Irrational Numbers:
Real numbers which can’t be communicated in the structure p/q and whose decimal expansions are non-ending and non-recurring.
Root values of primes like √2, √3, √5 and so forth are irrational
N is Natural Numbers:
The numbers that are countable are called natural numbers. N is equivalent to {1, 2, 3, … }
W is Whole Numbers:
Zero alongside every single natural number are together called whole numbers. {0, 1, 2, 3,… }
Even Numbers:
Natural numbers of the structure 2n are called even numbers. (2, 4, 6, … }
Odd Numbers:
Natural numbers of the structure 2n – 1 are called odd numbers. {1, 3, 5, … }
For what reason wouldn’t we be able to compose the structure as 2n+1?
Recall this!
Every single Natural Number are whole numbers.
Every single Whole Number are Integers.
All Integers are Rational Numbers.
Every single Rational Number are Real Numbers.
Prime Numbers:
The natural numbers more noteworthy than 1 which are divisible by 1 and the number itself are called prime numbers, Prime numbers have two factors i.e., 1 and the number itself, For instance, 2, 3, 5, 7 and 11 and so on.
1 is certifiably not a prime number as it has just one factor.
Composite Numbers:
The natural numbers which are divisible by 1, itself and some other number or numbers are called composite numbers. For instance, 4, 6, 8, 9, 10 and so on.
Note: 1 is neither composite nor a prime number.
-
Euclid’s Division lemma
Given two positive integers an and b, there exist one of a kind integers q and r fulfilling a = QB + r, 0 ≤ r ≤ b.
Notice this. Each time ‘r’ is not as much as b. Every ‘q’ and ‘r’ is one of a kind.

-
Use of lemma
Euclid’s Division lemma is utilized to discover HCF of two positive integers. Model: Find HCF of 56 and 72?
Steps:
Apply lemma to 56 and 72.
Take a greater number and find ‘b’ and ‘r’. 72 is equal 56 × 1 + 16
Since 16 ≠ 0, think about 56 as the net profit and 16 as the new divisor. 56 is equal to 16 × 3 + 8
Once more, 8 ≠ 0, think about 16 as new profit and 8 as new divisor. 16 is equal to 8 × 2 + 0
Since the remainder is zero, divisor (8) is the Highest Common Factor.
In spite of the fact that Euclid’s Division lemma is expressed for just positive integers, it very well may be reached out for all integers aside from zero, i.e., b ≠ 0.
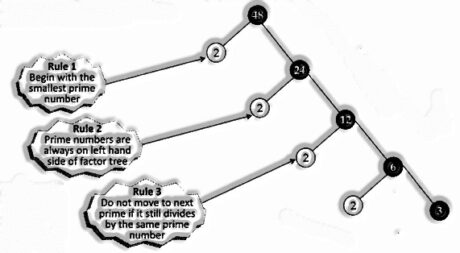
III. Developing a factor tree
Steps
Compose the number as a result of a prime number and a composite number
Model:
Factorize 48
Rehash the procedure till all the primes are acquired
∴ Prime factorization of 48 is equal to 24 x 3
-
The central hypothesis of Arithmetic
Each composite number can be communicated as a result of primes, and this articulation is one of a kind, aside from the request in which they show up.
Applications:
To find HCF and LCM of at least two positive integers.
To demonstrate the irrationality of numbers.
To decide the idea of the decimal expansion of rational numbers.
- The calculation to find HCF and LCM of at least two positive integers:
Step I:
Factorize every one of the given positive integers and express them as a result of powers of primes in a rising significant degree of primes.
Step II:
To discover HCF, distinguish normal prime factor and locate the least powers and increase them to get HCF.
Step III:
To discover LCM, locate the best exponent and afterwards increase them to get the LCM.
- To demonstrate Irrationality of numbers:
The addition or subtraction of a rational and an irrational number is irrational.
The multiplication or division of a non-zero rational number and an irrational number is irrational.
- To decide the idea of the decimal expansion of rational numbers:
Let x = p/q, p and q are co-primes, be a rational number whose decimal expansion ends. At that point the prime factorization of ‘q’ is of the structure 2m5n, m and n are non-negative integers.
Say x = p/q be a rational number to such a degree that the prime factorization of ‘q’ isn’t of the structure 2m5n, ‘m’ and ‘n’ being non-negative integers, at that point x has a non-ending rehashing decimal expansion.
Alert!
23 can be composed as: 23 = 2350
52 can be composed as: 52 = 2052

