Practical Geometry: Class 6 Maths NCERT Chapter 14

Key Features of NCERT Material for Class 6 Maths Chapter 14 – Practical Geometry

In the previous chapter 13, we studied about the symmetry of objects, it’s application and types. In chapter 14 of class 6 NCERT maths book: Practical Geometry, we will study different geometrical tools and construction of lines, circles, angles using geometrical tools.

Quick Revision notes

Practical geometry is a significant part of geometry. It deals with the study of the size, positions, shapes just as measurements of objects. For what reason do we study constructions? For instance, if a building needs to be constructed. One has to know the precise map of the building. Construction intends to draw the lines and angles precisely. Additionally to draw the maps, learning the fundamentals of constructions is critical. Let us find out about the constructions in geometry. 

 Geometrical Instruments 

Regardless of whether you need to draw a line segment or measure it, draw a circle or arcs, draw an angle, it can be very easily done with the assistance of geometrical tools. Let us examine the different geometrical instruments utilized in practical geometry. 

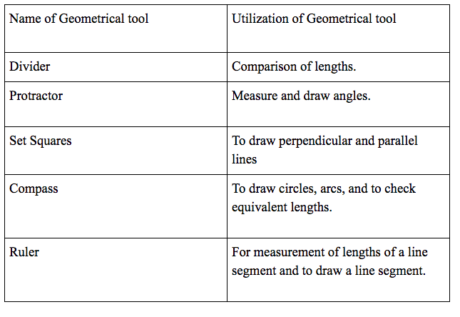
A ruler We utilize the accompanying instruments in drawing geometrical shapes: 

• The compasses 
• The divider 
• Set-squares, and 
• The protractor. 

In this section, we will learn only “Ruler-and-compass constructions”. 

Point  and Lines 

Point:

It is a location on a plane. 

Line:

Collection of points in a straight way that expands infinitely in two directions. 

Tools utilized for construction: 

• Rule. 
• Compass
• Divider:  
• Set-Squares 
• Protractor: 

Line Segment 

Line Segment: Part of a line that is limited by two unmistakable endpoints. 

We require a ruler here. 

Construction a line segment of the given length 

We need to utilize a ruler for this construction. Steps for drawing a line segment of a given length ‘a’: 

(I) Construct a line l and mark a point B on it. 

(ii) Place the compass on the underlying point of the ruler. Open it to put pencil point up to the ‘a’ mark. 

(iii) Place the pointer on A and construct an arc to cut l at B. AB is the necessary line segment. 

Constructing a duplicate of a given line segment.

We may utilize a ruler or trace paper here. Yet, it is better than we would utilize ruler and compasses for making the construction Steps for constructing a duplicate of a given line segment utilizing ruler and compass together: 

(I) Consider AB whose length is not known. 

(ii) Fix compass’ pointed end on A and pencil end on B. The opening of the instrument currently gives the length of AB. 

(iii) Construct any line l. 

(iv) Placing the pointer on C, draw an arc that intersects l at a point say D. At that point, line CD is equal to AB.

Circle 

Each point on the boundary of a circle is at an equivalent distance from the centre.

Development of a circle when the length of its radius is known 

We have to utilize compasses here. 

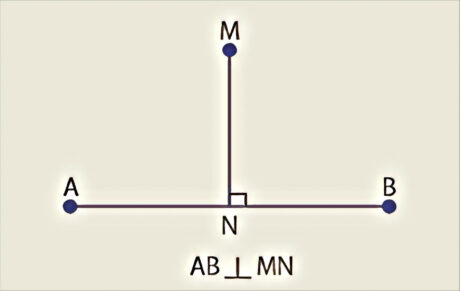
Perpendiculars 

Two lines or line segments or rays are supposed to be perpendicular on the off chance that they intersect with the end goal that the angle shaped between them is 90°. 

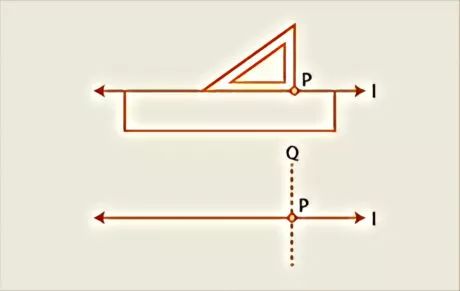
A Perpendicular drawn to a line through a point on the line

It might be done in three different ways: 

• by folding of paper, 
• utilizing a ruler and a set-square, and 
• utilizing a ruler and the compasses. 

A Perpendicular drawn to a line through a point not it 

Any of the three strategies given beneath can be used: 

• by paper folding, 
• utilizing a ruler and a set-square, and 
• utilizing a ruler and the compasses. 

Construction of perpendicular bisector of a line section 

There are three ways as given below: 

• by paper folding, 
• by utilizing transparent tapes, and 
• by utilizing ruler and compasses. 

Angles 

Angles are formed by two rays having a common endpoint.

Making an angle of a given measure 

We utilize a ruler and a protractor here. 

Constructing a duplicate of an angle of unknown measure 

We utilize a ruler (or a straight edge) and the compasses. 

Bisector of an angle 

Two techniques are possible: 

• by paper folding
• By utilizing ruler and compasses 
• Angles of special measures 

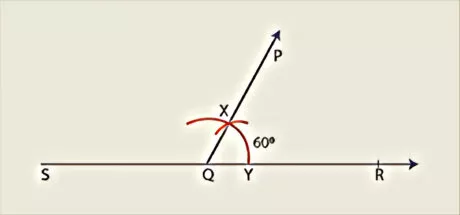
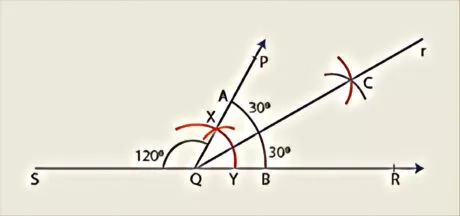
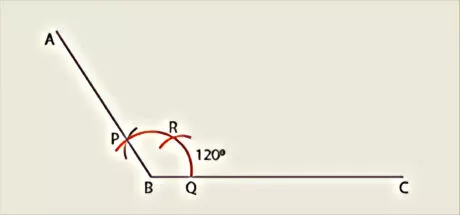
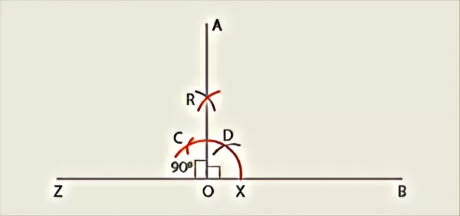
There are some precise and elegant techniques to build angles of special measures without utilizing the protractor. 

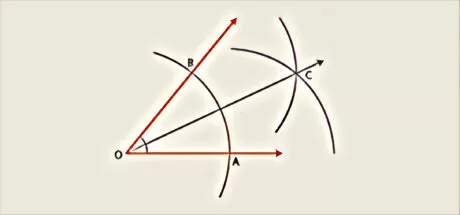
Some of them are: 

• 60° angle
•  30° angle construction
•  120° angle construction
•  90° angle construction