Polynomials: Class 10 Mathematics NCERT Chapter 2

Key Features of NCERT Material for Class 10 Mathematics Chapter 2 – Polynomials
In the last chapter 1: Real Numbers,you learned about Real numbers and their properties and get to know that how they can become useful to us. In this chapter: Polynomials, you will become familiar with the historical backdrop of Britain, “Polynomial” originates from the word ‘Poly’ (Meaning Many) and ‘nominal’ (for this situation significance Term)- so it implies numerous terms.
- A polynomial is comprised of terms that are just added, subtracted or multiplied.
- A quadratic polynomial in x with genuine coefficients is of the structure ax² + bx + c, where a, b, c are numbers with a ≠ 0.
- Degree – The most noteworthy exponent of the variable in the polynomial is known as the degree of polynomial. Model: 3×2 + 4, here degree = 2.
- Polynomials of degrees 1, 2 and 3 are called linear, quadratic and cubic polynomial individually.
- A polynomial can have terms which have Constants like 3, – 20, and so on., Variables like x and y and Exponents like 2 in y².
- These can be consolidated utilizing multiplication, addition and subtraction however NOT DIVISION.
- The zeroes of a polynomial p(x) are accurately the x-coordinates of the focuses, where the graph of y = p(x) converges the x-ordinate
Polynomial
An algebraic expression can possess exponents that are rational numbers. Be that as it may, a polynomial is an algebraic expression wherein the exponent on any variable is a whole number.
7×3+3x+1 is a case of a polynomial. However, It is an algebraic expression too.
2x+3√x is an algebraic expression, however not a polynomial. – since the exponent on x is 1/2 which is certainly not a whole number.
Degree of a Polynomial
For a polynomial in one variable – the most noteworthy exponent on the variable in a polynomial is the degree of the polynomial.
Model: The degree of the polynomial x2+2x+3 is 2, as the most noteworthy intensity of x in the given expression is x2.
Kinds OF POLYNOMIALS
Polynomials can be characterized dependent on:
a) Number of terms
b) Degree of the polynomial.
Kinds of polynomials dependent on the number of terms
a) Monomial – it is polynomial with only 1 term. Model: 2x, 6×2, 9xy
b) Binomial – A polynomial with two terms. Model: 4×2+x, 5x+4
a) Trinomial – A polynomial with three terms. Model: x2+3x+4
Kinds of Polynomials dependent on Degree
Linear Polynomial
A polynomial whose degree is one is known as a linear polynomial.
For instance, 2x+1 is a linear polynomial.
Quadratic Polynomial
A polynomial which has a degree of 2 is a quadratic polynomial.
For instance, 3×2+8x+5 is a quadratic polynomial.
Graphical Representations
Expressing Equations on a Graph
Any condition can be spoken to as a graph on the Cartesian plane, where each point on the graph shows the x and y coordinates of the point that fulfils the condition. A condition can be viewed as an imperative put on the x and y coordinates of a point, and any point that fulfils that limitation will lie on the curve.
For instance, the condition y = x, on a graph, will be a straight line that joins all the focuses which have their x coordinate equivalent to their y coordinate. Model – (2,2), (3,3, etc.
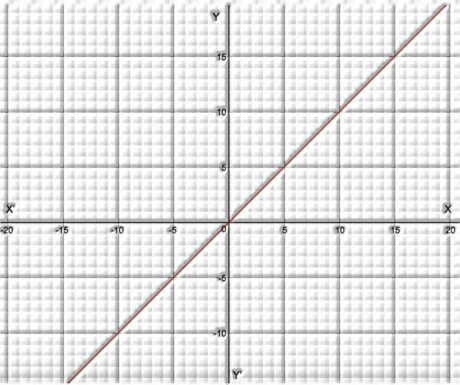
Graph of the polynomial Xn
For a polynomial of the structure y=xn where n is a whole number:
as n expands, the graph gets more extreme or moves nearer to the Y-pivot.
In the event that n is odd, the graph lines in the first and third quadrants
On the off chance that n is even, the graph lines in the first and second quadrants.
The graph of y=−xn is the reflection of the graph of y=xn on the x-pivot
Graph of polynomials with various degrees.
Zeroes of a Polynomial
A zero of a polynomial p(x) is the estimation of x for which the estimation of p(x) is 0. On the off chance that k is a zero of p(x), at that point p(k)=0.
For instance, consider a polynomial q(x)=x2−3x+2.
When x=1, the estimation of q(x) will be equivalent to
q(1)=12−3×1+2
q(1)=1−3+2
q(1)=0
Since q(x)=0 at x=1, we state that 1 is a zero of the polynomial x2−3x+2

Zeroes (α, β, γ) adhere to the standards of algebraic identities, i.e.,
(α + β)² is equal to α² + β² + 2αβ
∴(α² + β²) is equal to (α + β)² – 2αβ
DIVISION ALGORITHM:
In the event that p(x) and q(x) are any two polynomials with g(x) ≠ 0, at that point
p(x) = q(x) × g(x) + r(x)
The dividend is equal to Divisor x Quotient + Remainder
Recollect this!
On the off chance that r (x) = 0, at that point q (x) is a factor of p (x).
On the off chance that r (x) ≠ 0, at that point we can take away r (x) from p (x) and afterwards the new polynomial framed is a factor of q(x) and g(x).

