Pair of Linear Equations in Two Variables: Class 10 Mathematics NCERT Chapter 3

Key Features of NCERT Material for Class 10 Mathematics Chapter 3 – Pair of Linear equations in Two Variables
In the last chapter 2: Polynomials,you learned that “Polynomial” originates from the word ‘Poly’ (Meaning Many) and ‘nominal’ (for this situation significance Term)- so it implies numerous terms. In this chapter: Pair of Linear Equations in Two Variables, you will learn about linear equations that for any linear equation, every solution (x, y) compares to a point on the line. General structure is given by ax+ by + c = 0.
The graph of a linear equation is always expressed through a straight line.
Two linear equations in a similar two variables are known as a pair of linear equations in two variables. The most broad type of a pair of linear equations is: a1x + b1y + c1 = 0; a2x + b2y + c2 = 0
where a1, a2, b1, b2, c1 and c2 are real numbers, with the end goal that a12 + b12 ≠ 0, a22 + b22 ≠ 0.
A pair of values of variables ‘x’ and ‘y’ which fulfil both the equations in the given arrangement of equations is supposed to be a solution of the pair of linear equations.
A pair of linear equations in two variables can be solved and explained, by
(I) Graphical strategy
(ii) Algebraic strategy
Equation
An equation is an explanation that two mathematical expressions having at least one variables are equivalent.
Linear Equation
Equations in which the powers of variables included are one are called linear equations. The degree of a linear equation is consistently one.
General type of a Linear Equation in Two Variables
The overall type of a linear equation in two variables is ax+ by + c = 0, where a and b can’t be zero at the same time.
Depicting linear equations through a word problem
To depict through a word problem as a linear equation
Recognize obscure amounts and indicate them by variables.
Show connections between amounts in a mathematical structure, supplanting the unknowns with variables.
Solving a Linear Equation in 2 variables
The solution of a linear equation in two variables is a pair of values, one for x and the other for y, which makes the different sides of the equation equivalent.
Eg: If 3x+y=4, at that point (1,1) is one of its solutions as it fulfils the equation. A linear equation in two variables has interminably numerous solutions.
Geometrical Representation of a Linear Equation
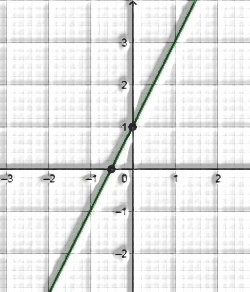
Geometrically, a linear equation in two variables can be shown as a straight line.
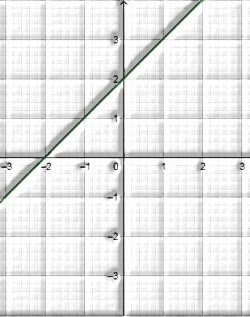
3x – y + 1 = 0
⇒ y = 3x + 1
Graph of y = 3x+1
Plotting a Straight Line

The graph of a linear equation in two variables is always represented through a straight line. We construct the straight line as follows:
Any extra focuses plotted as such will lie on a similar line.
About Lines
General type of a pair of linear equations in 2 variables
![]()
A pair of linear equations in two variables can be shown to as follows
The coefficients of x and y can’t be zero all the while for an equation.
Features of 2 straight lines in a plane
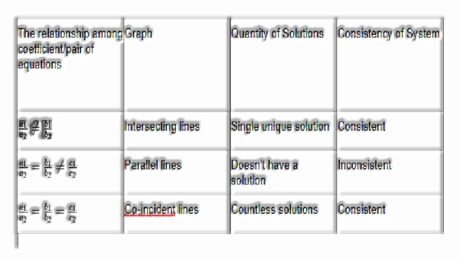
For a pair of straight lines on a plane, there are three prospects
I) They intersect at precisely one point
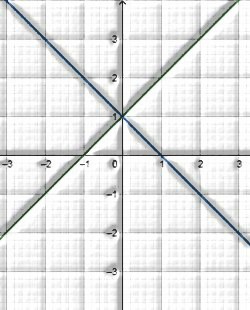
pair of linear equations which intersect at a solitary point.
ii) They are parallel
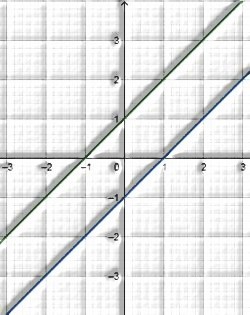
pair of linear equations which are said to be parallel.
iii) They are coincidental
pair of linear equations which are said to be coincidental.
Graphical Solution
Showing a pair of LE in 2 variables graphically
Graphically, a pair of linear equations in two variables can be expressed by a pair of straight lines.
A graphical technique for discovering the solution of a pair of Linear Equations
Graphical Method of finding the solution to a pair of linear equations is as per the following:
Plot both the equations (two straight lines)
Discover the point of the intersection of the lines.
The point of the intersection is said to be the solution.
Looking at the proportions of coefficients of a Linear Equation
Algebraic Solution

Discovering solution for consistent pair of Linear Equations
The solution of a pair of linear equations is of the structure (x,y) which fulfils both the equations at the same time. Solution for a consistent pair of linear equations can be discovered utilizing
I) Elimination strategy
ii) Substitution Method
iii) Cross-multiplication strategy
iv) Graphical strategy
(I) Graphical strategy. The graph of a pair of linear equations in two variables is introduced by two lines.
(ii) Algebraic strategies. Following are the techniques for finding the solutions(s) of a pair of linear equations:
Substitution strategy
Elimination strategy
Cross-multiplication strategy.
There are a few circumstances which can be mathematically expressed by two equations that are not linear, to begin with. In any case, we permit them with the goal that they are diminished to a pair of linear equations.
Consistent system. An arrangement of linear equations is supposed to be consistent on the off chance that it has one solution at least.
Inconsistent system. An arrangement of linear equations is supposed to be inconsistent on the off chance that it has no solution.
CONDITIONS FOR CONSISTENCY
Leave the two equations alone:
a1x + b1y + c1 = 0
a2x + b2y + c2 = 0
At that point,