Fractions Class 6 Maths NCERT Chapter 7

Key Features of NCERT Material for Class 6 Maths Chapter 7 – Fractions  

In the last chapter 6 Integers, We studied integers, representation of integers on a number line and mathematical operations on integers. In this chapter, we will study fractions, types of fractions and mathematical operations on different fractions

Quick revision notes

A fraction is a number signifying a part of the whole. The whole might be an object or a gathering of items. In other ways, we can say that a fraction is an operation on numbers.

A Fraction 

A fraction implies a piece of a group or of an area. ⅔   is a fraction. It is read as “Two-thirds”. 

    

Here, 4 represents the quantity of equivalent parts into which the entire has been separated and 3 represents the quantity which has been taken out. It is to be noticed that while communicating a circumstance of counting parts to compose a fraction, all parts must be equivalent. Here, 3 is known as the numerator and 4 is known as the denominator. Numerator and denominator can be recognized for any part. 

Fractions can be shown on a number line. Any fraction has a point related with it on the number line. 

Proper fraction:

We realize that a fraction basically has a numerator and a denominator which can be recognized for any division viable. When the numerator is lesser than the denominator, at that point the fraction is known as a proper fraction. 

For instance: 

½,⅔, ¾, and so forth. 

A fraction, whose numerator has a larger value than the denominator, is called an improper fraction. 

For instance: 7/2, 11/5 and so forth

Improper fractions can be composed as a blend of whole and a part, and are then called mixed fractions. 

For instance: when 5/4 composed as 1 ¼  is known as a mixed division. 

To communicate an inappropriate portion as a mixed fraction, we isolate the numerator by the denominator to get the remainder and the rest of. At that point, the mixed fraction can be composed as 

Quotient: Remainder/Divisor

To communicate a mixed fraction as an improper fraction, we multiply the whole number with the denominator and add the numerator to it. At that point, the mixed fraction can be composed as

(Whole× Denominator) + Numerator/ Denominator

Two fractions are supposed to be equal if they represent the same amount. Each proper and improper fraction has vastly numerous equivalent fractions. For finding an equivalent fraction of a given fraction, we have to multiply or divide both the numerator and the denominator of the given fraction by the equivalent nonzero number. In the event that two fractions are equal, at that point the result of the multiplication of numerator of the first and the denominator of the second is equivalent to the result of the multiplication of denominator of the first and the numerator of the second. This rule ends up being valuable to find equivalent fractions. 

The simplest form of a Fraction 

A fraction is supposed to be in the simplest (or least) form if its numerator and denominator have no common factor aside from 1, i.e., they are coprime natural numbers. Accordingly, to find the equivalent fraction in the simplest form, we have to find the HCF of the numerator and the denominator. At that point, we divide them by their HCF and get the equivalent fraction in simplest form. 

Like Fractions 

Fractions, whose denominators are the equivalent, are called Like fractions. 

For instance: 2/7, 4/7, 5/7 are like fractions while 2/7and 3/5 is not like fractions. The latter is known as unlike fractions as their denominators are not the same.

Comparing Fractions 

For fractions with similar numerators, the littler the denominator, the larger the fraction. 

For fractions with similar denominators, the larger the numerator, the larger the division. 

Comparison of  like fractions 

Like fractions are fractions with a similar denominator, in this way, to compare two like fractions, it is only adequate to look at their numerators. The greater the numerator, the larger the fraction. 

We realize that in two fractions with a similar denominator, the fraction with the greater numerator is bigger. Since in such cases the denominators are the equivalent, i.e., these are like fractions, subsequently, just numerators should be looked at, so these comparisons are relatively easy to make. 

Comparing unlike fractions 

We are aware that unlike fractions are fractions with different denominators. If their numerators are the equivalent, at that point littler the denominator, larger the fraction. In any case, if the two fractions have different numerators, at that point we find equivalent fractions of both and pick one from each to such an extent that their denominators are the equivalent. 

At that point for comparison, larger the numerator, larger the fraction. In this way, we can find the larger of the two given fractions with different numerators and denominators. 

In everyday life circumstances, We have to add or subtract the fractions sometimes. this is individually known as addition and subtraction of fractions. 

An instance of the addition of fractions is as per the following: 

Ravi purchased 2 ½ kg sugar while Meeta purchased 1 ½ kg sugar. Find the sum of sugar purchased by them. 

An instance of subtraction of fractions is as per the following: 

The professor taught ⅖ of the book. Seeta revised ⅖ more on her own. What amount does she still have to revise? 

Adding or Subtracting like fractions 

Addition of at least two like fractions can be done as follows: 

Step 1. Include the numerators. 

Step  2. Hold the denominator (normal). 

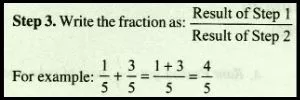
Subtraction of two fractions can be completed as follows: 

Step 1. Subtract the lesser numerator from the bigger numerator. 

Step 2. Hold the denominator (normal). 

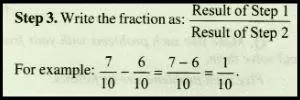
Adding and subtracting unlike fractions 

To add and subtract fractions that don’t have a similar denominator, we convert them into equivalent fractions with similar denominators and afterwards continue as above.

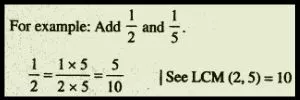
Multiplication of factors

Division of factors

Take the reciprocal (reverse) of one fraction and multiply with the other fraction

For instance:

1/3 ÷ 1/2
1/3 × Reciprocal of (1/2)
=1/3× 2 = (1×2)/3
=2/3