Coordinate Geometry: Class 10 Mathematics NCERT Chapter 7

Key Features of NCERT Material for Class 10 Mathematics Chapter 7 – Coordinate Geometry 

In the last chapter 6, you learned about everything about triangles. In this chapter, you will learn about Coordinate Geometry.

Position of a point P in the Cartesian plane as for coordinate axes is shown by the arranged pair (x, y). 

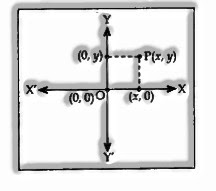
The line X’OX is said to be the X-axis and YOY’ is known as the Y-axis. The portion of intersection of the X-axis and Y-axis is known as the root O and the coordinates of O are (0, 0). 

The perpendicular distance of a point P from the Y-axis is the ‘x’ coordinate and is known as the abscissa. 

The perpendicular distance of a point P from the X-axis is the ‘y’ coordinate and is known as the ordinate. 

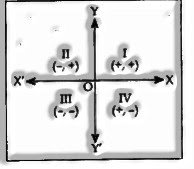
Indications of abscissa and ordinate in various quadrants are as given in the outline: 

Distance Formula 

Distance between Two differnt Points on the Same Coordinate Axes 

The distance between two points which are on a similar axis (x-axis or y-axis), is given by the distinction between their ordinates on the off chance that they are on the y-axis, else by the contrast between their abscissa on the off chance that they are on the x-axis. 

Distance AB is equal to 6 – (- 2) = 8 units 

Distance CD is equal to 4 – (- 8) = 12 units 

Distance between Two Points Using Pythagoras Theorem 

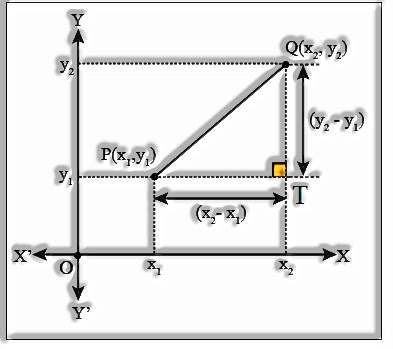
Discovering distance between 2 points utilizing 

Pythagoras Theorem 

Let P(x1, y1) and Q(x2, y2) be any two points on the cartesian plane. 

Attract lines corresponding to the tomahawks through P and Q to meet at T. 

ΔPTQ is a right triangle angled at T. 

By Pythagoras Theorem, 

PQ2 = PT2 + QT2 

= (x2 – x1)2 + (y2 – y1)2 

PQ 

=√[x2 – x1)2 + (y2 – y1)2] 

Distance Formula 

Distance between any distinct two points (x1, y1) and (x2, y2) is given by 

d = √[x2 – x1)2+(y2 – y1)2] 

Where d is the distance between the points (x1,y1) and (x2,y2). 

Any point on the X-axis is in the form(x, 0). 

Any point on the Y-axis is in the form(0, y). 

The distance between two distinctive points P(x1, y1) and Q (x2, y2) is given by 

PQ =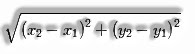 

Section formula

. The coordinates of the point which separates the line segment joining the points A(x1, y1) and B(x2, y2) inside in the ratio m : n are: 

The above formula is section equation. The proportion m: n can likewise be composed as : 1 or k : 1, The 

coordinates of P can likewise be composed as P(x,y) = 

The midpoint of the line segment connecting the points P(x1, y1) and Q(x2, y2) is 

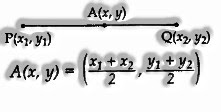
Here m : n = :1. 

Area of a Triangle. The area of a triangle shaped by points A(x1 y1), B(x2, y2) and C(x3, y3) is given by | ∆ |, 

where ∆ = 

where ∆ speaks to the outright worth. 

Three points are collinear if |A| = 0. 

On the off chance that P is centroid of a triangle, at that point the middle partitions it in the proportion 2 :1. Coordinates of P are given by

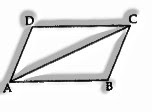
Area of a quadrilateral, ABCD is equal to ar(∆ABC) + ar(∆ADC) 

Discovering ratio given the points 

To discover the ratio wherein a given point P(x, y) separates the line segment joining A(x1, y1) and B(x2, y2), 

Accept that the proportion is k : 1 

Replace the ratio in the section formula for any of the coordinates to get the estimation of k. 

\(x=\frac{kx_{2}+x_{1}}{k+1}\) 

When x1, x2 and x are known, k can be determined. The equivalent can be determined from the y-coordinate too. 

MidPoint 

The midpoint of any line segment partitions it in the proportion 1 : 1. 

The coordinates of the midpoint(P) of line segment joining A(x1, y1) and B(x2, y2) is given by 

\(p(x,\ y)=(\frac{x_{1}+x_{2}}{2},\frac{y_{1}+y_{2}}{2} )\)