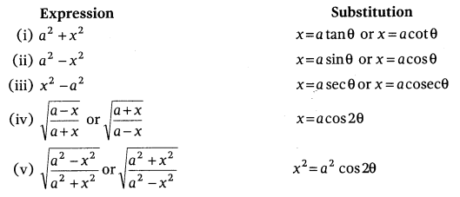Continuity and Differentiability:Class 12 Maths NCERT Chapter 5

Key Features of NCERT Material for Class 12 Maths Chapter 5 – Continuity and Differentiability

In the previous Chapter 4:Determinants we have learned about determinants and properties of determinants.In this Chapter 5:Continuity and Differentiability,we will learn about continuity, algebra of continuous function.

Quick revision notes

Continuity at a Point: A function f(x) is supposed to be continuous at a point x = an, if 

Left hand limit of f(x) at(x = a) = Right hand limit of f(x) when (x = a) = Value of f(x) at (x = a) 

for example on the off chance that at x = a, LHL = RHL = f(a) 

where, LHL =

  and RHL =

Note: To assess LHL of a function f(x) at (x = o), put x = a – h and to discover RHL, put x = a + h. 

Continuity in an Interval: A function y = f(x) is supposed to be continuous in an interval (a, b), where a < b if and just if f(x) is continuous at each point in that interval. 

• Every identity function is continuous.
• Every constant function is continuous.
• Every polynomial function is continuous.
• Every rational function is continuous.
• All trigonometric functions are continuous in their domain.

Standard Results of Limits

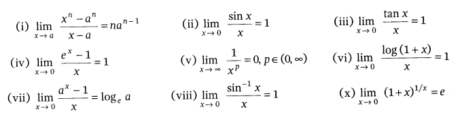
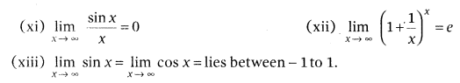
Algebra of Continuous Functions

Suppose f and g are two real functions, continuous at real number c. Then we have,

• f + g is continuous at x = c.
• f – g is continuous at x = c.
• f.g is continuous at x = c.
• cf is continuous, where c is any constant.
• (f/g) is continuous at x = c, [provide g(c) ≠ 0]

Suppose f and g are two real valued functions such that (fog) is defined at c. If g is continuous at c and f is continuous at g (c), then we have (fog) is continuous at c.

If f is continuous,also then |f| is continuous.

Differentiability: A function f(x) is supposed to be differentiable at a point x = an, if  Left hand derivative when (x = a) = Right hand derivative when (x = a) for example LHD at (x = a) = RHD (at x = a), where,

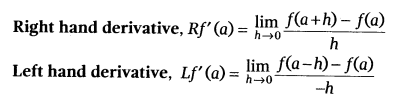
Note: Every differentiable function is continuous yet every continuous function isn’t differentiable. 

Separation: The way toward finding a derivative of a function is called separation. 

Rules of Differentiation 

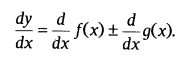
Sum and Difference Rule: Let y = f(x) ± g(x).Then, by utilizing sum and contrast rule, it’s derivative is composed as

Product Rule:  Let y = f(x) g(x). At that point, by utilizing item rule, it’s derivative is composed as 

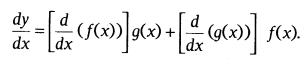
Quotient Rule: Let y = f(x)/g(x); g(x) ≠ 0, at that point by utilizing remainder rule, it’s derivative is composed as 

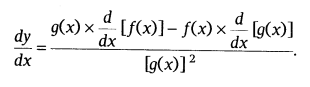
Chain Rule: Let y = f(u) and u = f(x), then by using chain rule, we may compose

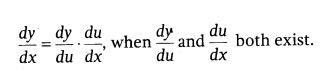
Logarithmic Differentiation: Let y = [f(x)]g(x) ..(i)

So by taking log (to base e) we can compose Eq. (i) as log y = g(x) log f(x). At that point , by utilising chain rule

Differentiation of Functions in Parametric Form: A relation expressed between two variables x and y in the form x = f(t), y = g(t) is said to be parametric form with t as a parameter, when we have

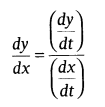
(whenever )

Note: dy/dx is communicated as far as boundary just without legitimately including the primary variables x and y. 

Second order Derivative: It is the derivative of the first order derivative.

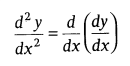
Some Standard Derivatives

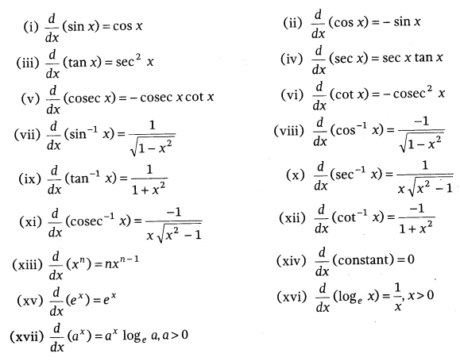
Rolle’s Theorem: Let f : [a, b] → R be continuous on [a, b] and differentiable on (a, b) with the end goal that f(a) = f(b), where a and b are some real numbers. At that point, there exists at least one number c in (a, b) such that f'(c) = 0.

Mean Value Theorem: Let f : [a, b] → R be continuous function on [a, b]and differentiable on (a, b). At that point, there exists at least one number c in (a, b) with the end goal that

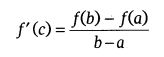
Note: Mean value theorem is an expansion of Rolle’s theorem.

Some Useful Substitutions for Finding Derivatives Expression