Circles: Class 10 Mathematics NCERT Chapter 10

Key Features of NCERT Material for Class 10 Mathematics Chapter 10 – Circles

In the last chapter 9, you learned about Some Applications of Trigonometry. In this chapter, you will learn about Circle. Circle: A circle is an assortment of all points in a plane which are at a steady distance from a fixed point. 

For a circle and a line on a plane, there can be three prospects. 

I) they can be non-intersecting 

ii) they may have a common point: for this situation, the line contacts the circle. 

ii) they can have two common points: for this situation, the line cuts the circle. 

Focus: The fixed point is known as the focus. 

Radius: The steady distance from the middle is known as the radius. 

Chord: A line segment joining any two points on a circle is known as a chord. 

Diameter: A chord going through the focal point of the circle is called diameter. It is the longest chord. 

Tangent: When a line meets the circle at one point or two coincidences The line is known as points, a tangent. 

The tangent to a circle is said to be perpendicular to the radius through the point of contact. 

⇒ OP ⊥ AB 

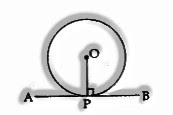
The lengths of the two tangents from an external point to a circle are equivalent. 

⇒ AP = PB 

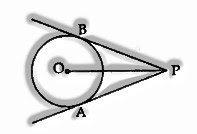
Length of Tangent Segment 

PB and PA are typically called the lengths of tangents from outside point P. 

Properties of Tangent to Circle 

Hypothesis 1: Prove that the tangent anytime of a circle is perpendicular to the radius through the point of contact. 

Given: XY is a tangent at point P to the circle with focus O. 

To demonstrate: OP ⊥ XY 

Construct: Take a point Q on XY other than P and join OQ 

Evidence: If point Q lies inside the circle, at that point XY will turn into a secant and not a tangent to the circle 

OQ > OP 

This occurs with each point on the line XY aside from the point P. Operation is the most brief of the apparent multitude of distances of the point O to the points of XY 

Operation ⊥ XY … [Shortest side is the perpendicular] 

Hypothesis 2: A line drawn through the end point of a radius and perpendicular to it, is the tangent to the circle. 

Given: A circle C(O, r) and a line APB is perpendicular to OP,  and here OP is the radius. 

To demonstrate: AB is tangent at P. 

Construct: Take a point Q on the line AB, unique in relation to P and join OQ. 

Verification: Since OP ⊥ AB 

OP < OQ ⇒ OQ > OP 

The point Q lies outside the circle. 

Accordingly, every point on AB, other than P, lies outside the circle. 

This shows AB meets the circle at point P. 

Consequently, AP is a tangent to the circle at P. 

Hypothesis 3: Prove that the lengths of tangents drawn from an external point to a circle are equivalent 

Given: PT and PS are tangents from an external point P to the circle with focus O. 

To demonstrate: PT = PS 

Construct: Join O to P, T and S. 

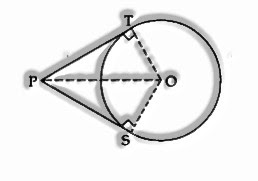
Verification: In ∆OTP and ∆OSP. 

OT = OS … [radii of the equivalent circle] 

Operation = OP … [common] 

∠OTP = ∠OSP … [each 90°] 

∆OTP = ∆OSP … [R.H.S.] 

PT = PS … [c.p.c.t.] 

Note: If two tangents are attracted to a circle from an external point, at that point: 

They subtend equivalent angles at the inside i.e., ∠1 = ∠2. 

They are similarly disposed to the segment joining the middle to that point i.e., ∠3 = ∠4. 

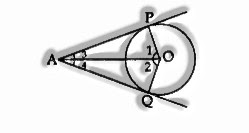
∠OAP = ∠OAQ